题目内容
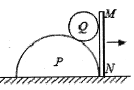
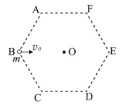
【题目】如图甲所示，粗糙水平面与竖直的光滑半圆环在N点相切，M为圈环的最高点，圆环半径为R=0.1m，现有一质量m=1kg的物体以v0=4m/s的初速度从水平面的某点向右运动并冲上竖直光滑半圆环，取g=10m/s2，求：
（1）物体能从M点飞出，落到水平面时落点到N点的距离的最小值Xm
（2）设出发点到N点的距离为S，物体从M点飞出后，落到水平面时落点到N点的距离为X，作出X2随S变化的关系如图乙所示，求物体与水平面间的动摩擦因数μ
（3）要使物体从某点出发后的运动过程中不会在N到M点的中间离开半固轨道，求出发点到N点的距离S应满足的条件
【答案】（1）0.2m；（2）0.2；（3）0≤x≤2.75m或3.5m≤x＜4m．
【解析】
（1）由牛顿第二定律求得在M点的速度范围，然后由平抛运动规律求得水平位移，即可得到最小值；
（2）根据动能定理得到M点速度和x的关系，然后由平抛运动规律得到y和M点速度的关系，即可得到y和x的关系，结合图象求解；
（3）根据物体不脱离轨道得到运动过程，然后由动能定理求解．
（1）物体能从M点飞出，那么对物体在M点应用牛顿第二定律可得：mg≤
，所以，vM≥
＝1m/s；
物体能从M点飞出做平抛运动，故有：2R＝
gt2，落到水平面时落点到N点的距离x＝vMt≥
＝2R＝0.2m；
故落到水平面时落点到N点的距离的最小值为0.2m；
（2）物体从出发点到M的运动过程作用摩擦力、重力做功，故由动能定理可得：μmgx2mgR＝mvM2mv02；
物体从M点落回水平面做平抛运动，故有：2R＝gt2，
；
由图可得：y2=0.48-0.16x，所以，μ＝
＝0.2；
（3）要使物体从某点出发后的运动过程中不会在N到M点的中间离开半圆轨道，那么物体能到达的最大高度0＜h≤R或物体能通过M点；
物体能到达的最大高度0＜h≤R时，由动能定理可得：μmgxmgh＝0mv02，
所以，
，
所以，3.5m≤x＜4m；
物体能通过M点时，由（1）可知vM≥＝1m/s，
由动能定理可得：μmgx2mgR＝mvM2mv02；
所以
，
所以，0≤x≤2.75m；
