题目内容
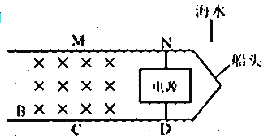
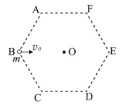
【题目】如图所示,在竖直面内有一边长为![]() 的正六边形区域,O为中心点,CD水平。将一质量为m的小球以一定的初动能从B点水平向右拋出,小球运动轨迹过D点。现在该竖直面内加一匀强电场,并让该小球带电,电荷量为+q,并以前述初动能沿各个方向从B点拋入六边形区域,小球将沿不同轨迹运动。已知某一方向拋入的小球过O点时动能为初动能的
的正六边形区域,O为中心点,CD水平。将一质量为m的小球以一定的初动能从B点水平向右拋出,小球运动轨迹过D点。现在该竖直面内加一匀强电场,并让该小球带电,电荷量为+q,并以前述初动能沿各个方向从B点拋入六边形区域,小球将沿不同轨迹运动。已知某一方向拋入的小球过O点时动能为初动能的![]() ,另一方向拋入的小球过C点时动能与初动能相等。重力加速度为g,电场区域足够大,求:
,另一方向拋入的小球过C点时动能与初动能相等。重力加速度为g,电场区域足够大,求:
(1)小球的初动能;
(2)取电场中B点的电势为零,求O、C两点的电势;
(3)已知小球从某一特定方向从B点拋入六边形区域后,小球将会再次回到B,求该特定方向拋入的小球在六边形区域内运动的时间。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)设小球从B点抛出时速度为![]() ,从B到D所用时间为t,小球做平抛运动
,从B到D所用时间为t,小球做平抛运动
在水平方向上![]()
在竖直方向上![]()
由几何关系可知:![]() ,
,![]()
解得小球的初动能为:![]()
(2)带电小球B→O:由动能定理得:![]()
![]()
解得:![]()
带电小球B→C:由动能定理得:![]()
![]()
解得:![]()
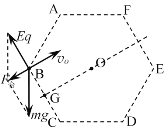
(3)在正六边形的BC边上取一点G,令![]() ,设G到B的距离为x,则由匀强电场性质可知
,设G到B的距离为x,则由匀强电场性质可知
![]()
解得:![]()
由几何知识可得,直线GO与正六边形的BC边垂直,OG为等势线,电场方向沿CB方向,由匀强电场电场强度与电势的关系可得
![]()
受力分析如图,根据力合成的平行四边形定则可得:![]() ,方向F→B
,方向F→B
小球只有沿BF方向抛入的小球才会再次回到B点,该小球进入六边形区域后,做匀减速直线运动,速度减为零后反向匀加速直线运动回到B点,设匀减速所用时间为t1,匀加速所用时间为t2,匀减速发生的位移为x
![]()
由牛顿定律得![]()
![]() (未射出六边形区域)
(未射出六边形区域)
小球在六边形区域内运动时间为![]()

练习册系列答案
相关题目