题目内容
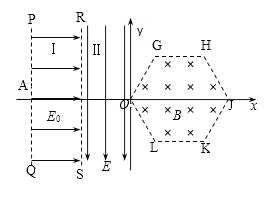
【题目】如图所示,xOy平面内,直线PQ、RS与y轴平行,PQ与RS 、RS与y轴之间的距离均为d。PQ、RS之间的足够大区域Ⅰ内有沿x轴正方向的匀强电场,场强大小为![]() ,RS与y轴之间的足够大区域Ⅱ内有沿y轴负方向的匀强电场。y轴右侧边长为d的正六边形OGHJKL区域内有垂直于xOy平面向里的匀强磁场,正六边形OGHJKL的O点位于坐标原点,J点位于x轴上。现将一电荷量为q,质量为m的带正电粒子从直线PQ上的某点A由静止释放,经PQ与RS之间的电场加速、RS与y轴之间的电场偏转后从坐标原点O点进入匀强磁场区域,经磁场区域后从正六边形的H点沿y轴正方向离开磁场。不计粒子所受重力,整个装置处在真空中,粒子运动的轨迹在xOy平面内。求:
,RS与y轴之间的足够大区域Ⅱ内有沿y轴负方向的匀强电场。y轴右侧边长为d的正六边形OGHJKL区域内有垂直于xOy平面向里的匀强磁场,正六边形OGHJKL的O点位于坐标原点,J点位于x轴上。现将一电荷量为q,质量为m的带正电粒子从直线PQ上的某点A由静止释放,经PQ与RS之间的电场加速、RS与y轴之间的电场偏转后从坐标原点O点进入匀强磁场区域,经磁场区域后从正六边形的H点沿y轴正方向离开磁场。不计粒子所受重力,整个装置处在真空中,粒子运动的轨迹在xOy平面内。求:
(1)粒子经直线RS从电场区域Ⅰ进入电场区域Ⅱ时的速度大小;
(2)电场区域Ⅱ的场强大小;
(3)磁场的磁感应强度大小。
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】试题分析:(1)粒子在电场力运动,电场力做正功,由动能定理即可求解运动的速度;(2)由由题意画出粒子在电、磁场中运动的轨迹图,并根据粒子在电场、磁场中运动的特点求解电场强度和磁感应强度。
(1)设粒子进入电场区域Ⅱ时的速度大小为v0,由动能定理得:![]()
解得:![]()
(2)由题意画出粒子在电、磁场中运动的轨迹如图所示
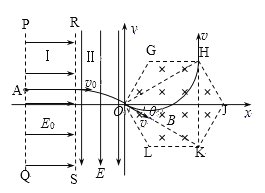
根据带电粒子在匀强磁场中做匀速圆周运动的特点及几何知识可知,粒子进入磁场时的速度方向与x轴的夹角![]()
设Ⅱ区电场强度大小为E,粒子进入磁场时的速度大小为v,在y轴方向的分速度为![]() ,粒子在Ⅱ区运动加速度为
,粒子在Ⅱ区运动加速度为![]() ,时间为t
,时间为t
由牛顿第二定律及匀变速运动规律得:![]() ,
,![]() ,
,![]() ,
,![]()
联立以上各式解得:![]()
(3)由根据带电粒子在匀强磁场中做匀速圆周运动的特点及几何知识可知,电粒子在匀强磁场中做匀速圆周运动的轨道半径:![]()
由洛伦兹力提供向心力得:![]()
由运动合成可知:![]()
联立以上各式解得:![]()

【题目】为了探究受到空气阻力时,物体运动速度随时间的变化规律,某同学采用了“加速度与物体质量、物体受力关系”的实验装置(如图所示).实验时,平衡小车与木板之间的摩擦力后,在小车上安装一薄板,以增大空气对小车运动的阻力.
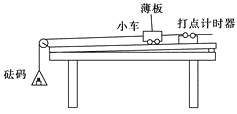
(1)往砝码盘中加入一小砝码,在释放小车________(选填“之前”或“之后”)接通打点计时器的电源,在纸带上打出一系列的点.
(2)从纸带上选取若干计数点进行测量,得出各计数点的时间t与速度v的数据如下表:
时间t/s | 0 | 0.50 | 1.00 | 1.50 | 2.00 | 2.50 |
速度v/(m·s-1) | 0.12 | 0.19 | 0.23 | 0.26 | 0.28 | 0.29 |
请根据实验数据作出小车的v-t图象.
(3)通过对实验结果的分析,该同学认为:随着运动速度的增加,小车所受的空气阻力将变大.你是否同意他的观点?请根据v-t图象简要阐述理由.