题目内容
18.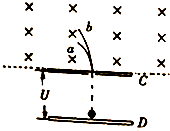 如图,一对水平放置的平行放置的平行金属板C、D始终与一直流电源两级相连,在C板上方存在一纸面向里的匀强磁场,在D板中央附近有一能发出a、b两种带电粒子的粒子源,而在C板上正对着粒子源处有一小孔,若a、b两种带电粒子经电场加速后,从C板上的小孔进入磁场的部分运动轨迹如图所示,则( )
如图,一对水平放置的平行放置的平行金属板C、D始终与一直流电源两级相连,在C板上方存在一纸面向里的匀强磁场,在D板中央附近有一能发出a、b两种带电粒子的粒子源,而在C板上正对着粒子源处有一小孔,若a、b两种带电粒子经电场加速后,从C板上的小孔进入磁场的部分运动轨迹如图所示,则( )| A. | C板一定与电源的正极相连 | |
| B. | 带电粒子a的比荷一定比带电粒子b的比荷大 | |
| C. | 在磁场中,带电粒子a一定的时间与带电粒子b一定的时间相等 | |
| D. | 带电粒子a进入磁场时的动能一定比带电粒子b进入磁场时的动能大 |
分析 粒子在电场中加速,在磁场中做匀速圆周运动,根据图示确定两粒子间的轨道半径大小关系,然后应用动能定理与牛顿第二定律分析答题.
解答 解:A、由图示可知,粒子进入磁场后向左偏转,粒子刚进入磁场时受到的洛伦兹力水平向左,由左手定则可知粒子带正电,粒子在D、C两板间加速,则D与电源正极相连,C与电源负极相连,故A错误;
B、粒子在电场中加速,由动能定理得:qU=$\frac{1}{2}$mv2-0,粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,解得:r=$\frac{1}{B}$$\sqrt{\frac{2mU}{q}}$,由图示可知,a的轨道半径小于b的轨道半径,则a的比荷比b的比荷大,故B正确;
C、粒子在磁场中做圆周运动的周期:T=$\frac{2πm}{qB}$,a的比荷比b的比荷大,则a在周期比b的周期小,即:Ta<Tb,a、b在磁场中的运动时间都是半个周期,则a的运动时间小于b的运动时间,故C错误;
D、粒子在电场中加速,由动能定理得:qU=$\frac{1}{2}$mv2-0,粒子进入磁场时的动能:EK=qU,U相同而不知道两粒子电荷量q的关系,无法确定粒子进入磁场时的动能关系,故D错误;
故选:B.
点评 本题考查了粒子在磁场中的运动,分析清楚粒子运动过程、根据图示确定两粒子在磁场中做圆周运动的轨道半径关系是解题的关键.

练习册系列答案
相关题目
8.在电磁波谱中,红外线、可见光和伦琴射线(X射线)三个波段的频率大小关系是( )
| A. | 红外线的频率最大,可见光的频率最小 | |
| B. | 伦琴射线的频率最大,红外线的频率最小 | |
| C. | 可见光的频率最大,红外线的频率最大 | |
| D. | 伦琴射线频率最大,可见光的频率最小 |
9.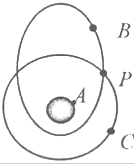 如图所示,A为静止于地球赤道上的物体,B为绕地球沿椭圆轨道运行的卫星,C为绕地球质量做圆周运动的卫星,P为B、C两卫星轨道的交点,已知A、B、C绕地心运动的周期T相同,相对地心,下列说法中正确的是( )
如图所示,A为静止于地球赤道上的物体,B为绕地球沿椭圆轨道运行的卫星,C为绕地球质量做圆周运动的卫星,P为B、C两卫星轨道的交点,已知A、B、C绕地心运动的周期T相同,相对地心,下列说法中正确的是( )
 如图所示,A为静止于地球赤道上的物体,B为绕地球沿椭圆轨道运行的卫星,C为绕地球质量做圆周运动的卫星,P为B、C两卫星轨道的交点,已知A、B、C绕地心运动的周期T相同,相对地心,下列说法中正确的是( )
如图所示,A为静止于地球赤道上的物体,B为绕地球沿椭圆轨道运行的卫星,C为绕地球质量做圆周运动的卫星,P为B、C两卫星轨道的交点,已知A、B、C绕地心运动的周期T相同,相对地心,下列说法中正确的是( )| A. | 物体A和卫星C具有相同大小的加速度 | |
| B. | 卫星B的周期T等于24小时 | |
| C. | 可能出现:在每天的某一固定时刻卫星B在A的正上方 | |
| D. | 卫星B的椭圆轨道的长半轴长度比卫星C的圆轨道的半径大 |
13.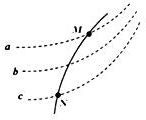 如图所示,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点(不计重力)仅在电场力作用下通过该区域时的运动轨迹,M、N是这条轨迹上的两点,据此可知正确的是( )
如图所示,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点(不计重力)仅在电场力作用下通过该区域时的运动轨迹,M、N是这条轨迹上的两点,据此可知正确的是( )
 如图所示,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点(不计重力)仅在电场力作用下通过该区域时的运动轨迹,M、N是这条轨迹上的两点,据此可知正确的是( )
如图所示,虚线a、b、c代表电场中三个等势面,相邻等势面之间的电势差相等,即Uab=Ubc,实线为一带正电的质点(不计重力)仅在电场力作用下通过该区域时的运动轨迹,M、N是这条轨迹上的两点,据此可知正确的是( )| A. | 三个等势面中的,a的电势最高 | |
| B. | 带电质点通过M点时的动能比经过N点时小 | |
| C. | 带电质点通过M点时的加速度比经过N点时小 | |
| D. | 带电质点一定是从M点沿着实线向N点运动 |
3.下列说法正确的是( )
| A. | 原来有某种放射性元素的原子核500个,经过1个半衰期T后,一定仅剩250个该发射性原子核未发生衰变 | |
| B. | 光电效应实验中,光电子的最大初动能与入射光的频率有关 | |
| C. | 天然发射现象中发射出的α、β、γ三种射线,γ射线的穿透能力最强 | |
| D. | 结合能越大,表示原子核结合得越牢固 | |
| E. | 根据波尔理论,氢原子的核外电子由高能级跃迁到低能级时,要释放出一定频率的光子,同时电子的动能增加,势能减少 |
10.一小球自地面上方某高度处自由下落,测得小球在最后1s内的位移是35m,不计空气阻力,g取10m/s2,则( )
| A. | 小球从释放到落地的时间为5s | B. | 小球从释放到落地的时间为4s | ||
| C. | 小球释放点距地面的高度为125m | D. | 小球释放点距地面的高度为80m |
7.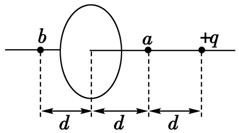 如图所示,有一带电量为+q的点电荷与均匀带电的圆形薄板相距为2d,圆形薄板带电量为-Q,点电荷到带电薄板的垂线通过板的圆心,若图中b点处的电场强度为零,则图中a点处的电场强度大小是( )
如图所示,有一带电量为+q的点电荷与均匀带电的圆形薄板相距为2d,圆形薄板带电量为-Q,点电荷到带电薄板的垂线通过板的圆心,若图中b点处的电场强度为零,则图中a点处的电场强度大小是( )
 如图所示,有一带电量为+q的点电荷与均匀带电的圆形薄板相距为2d,圆形薄板带电量为-Q,点电荷到带电薄板的垂线通过板的圆心,若图中b点处的电场强度为零,则图中a点处的电场强度大小是( )
如图所示,有一带电量为+q的点电荷与均匀带电的圆形薄板相距为2d,圆形薄板带电量为-Q,点电荷到带电薄板的垂线通过板的圆心,若图中b点处的电场强度为零,则图中a点处的电场强度大小是( )| A. | $\frac{10kq}{9{d}^{2}}$ | B. | $\frac{8kq}{9{d}^{2}}$ | C. | $\frac{k(Q+q)}{{d}^{2}}$ | D. | $\frac{kq}{{d}^{2}}$ |
8.下列过程中,物体机械能不守恒的是( )
| A. | 降落伞在空中匀速下落 | |
| B. | 物体在光滑斜面上自由下滑 | |
| C. | 小球被平抛后在空中运动的过程 | |
| D. | 物体在拉力作用下,在粗糙水平面上匀速运动 |
