题目内容
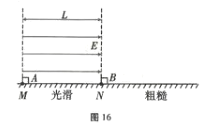
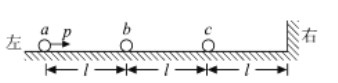
【题目】大小相同的三个小球(可视为质点)a、b、c静止在光滑水平面上,依次相距l等距离排列成一条直线,在c右侧距c为l处有一竖直墙,墙面垂直小球连线,如图所示。小球a的质量为2m,b、c的质量均为m。某时刻给a一沿连线向右的初动量p,忽略空气阻力、碰撞中的动能损失和碰撞时间。下列判断正确的是( )
A.c第一次被碰后瞬间的动能为![]()
B.c第一次被碰后瞬间的动能为![]()
C.a与b第二次碰撞处距竖直墙的距离为![]()
D.a与b第二次碰撞处距竖直墙的距离为![]()
【答案】AC
【解析】
a球与b球发生弹性碰撞,设a球碰前的初速度为v0,碰后a、b的速度为![]() 、
、![]() ,取向右为正,由动量守恒定律和能量守恒定律有
,取向右为正,由动量守恒定律和能量守恒定律有
![]()
![]()
其中![]() ,解得
,解得
![]() ,
,![]()
b球以速度v2与静止的c球发生弹性碰撞,设碰后的速度为![]() 、
、![]() ,根据等质量的两个球发生动静弹性碰撞,会出现速度交换,故有
,根据等质量的两个球发生动静弹性碰撞,会出现速度交换,故有
![]() ,
,![]()
AB.c第一次被碰后瞬间的动能为
![]()
故A正确,B错误;
CD.设a与b第二次碰撞的位置距离c停的位置为![]() ,两次碰撞的时间间隔为t,b球以v2向右运动l与c碰撞,c以一样的速度v4运动2l的距离返回与b弹碰,b再次获得v4向左运动直到与a第二次碰撞,有
,两次碰撞的时间间隔为t,b球以v2向右运动l与c碰撞,c以一样的速度v4运动2l的距离返回与b弹碰,b再次获得v4向左运动直到与a第二次碰撞,有
![]()
对a球在相同的时间内有
![]()
联立可得![]() ,故a与b第二次碰撞处距竖直墙的距离为
,故a与b第二次碰撞处距竖直墙的距离为
![]()
故C正确,D错误。
故选AC。

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目