题目内容
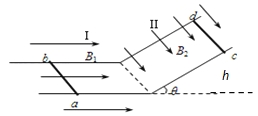
【题目】如图所示，边长为L的正三角形abc区域内存在垂直纸面向里的的匀强磁场，质量为m，电荷量均为q的三个粒子A、B、C以大小不等的速度从a点沿与ab边成30°角的方向垂直射入磁场后从ac边界穿出，穿出ac边界时与a点的距离分别为
、
、L。不及粒子的重力及粒子间的相互作用，则下列说法正确的是
A. 粒子C在磁场中做圆周运动的半径为L
B. A、B、C三个粒子的初速度大小之比为3:2:1
C. A、B、C三个粒子从磁场中射出的方向均与ab边垂直
D. 仅将磁场的磁感应强度减小
，则粒子B从c点射出
【答案】ACD
【解析】A、由圆周运动的对称性可知，同一直线边界以30°的弦切角进磁场，射出时的速度也与边界成30°，而圆心角为60°，则圆心和入射点以及出射点构成等边三角形，由几何关系可知
，
，
，故A正确。B、根据洛伦兹力提供向心力有
，可知
，可得初速度之比
，B错误。C、由于三粒子从ac出射时夹角为30°，而
，故出射速度的延长线必与ab边垂直构成直角三角形，故C正确。D、由
可知将B改为
，半径将变为
，而其它条件不变，故由几何关系可知B粒子将从c点出射，D正确。故选ACD.
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
