��Ŀ����
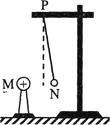
����Ŀ�������ӵ���ǧ����ij��Ϸ�ŵľ��������Ŀ����ͼ��ʾ����ظ�H=5.4m��O��̶�һ����L=3.6m�Ҳ����쳤����������������һ����һƽ̨����ֱ���ӣ���ĩ������λ��ƽ̨��ԵA�㣬��������ֱ�����60��ǣ���һ����m=5kg�ĺ�����A��ץס����ĩ�����ٶȵ��뿪ƽ̨�����˶������к��ӿ���Ϊ�ʵ㣬�����������ƣ���gȡ10m/s2��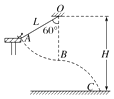
��1�����Ӿ���O�����·�B��ʱ���ٶȴ�С��
��2�����Ӿ���O�����·�B��ʱ�ܵ����ӵ�������С��
��3����������B��ſ����ӣ�������ص�C������O���ˮƽ������
��4��������������������һ���������ѵ��Ա�İ�������������ֱ�����60��ǣ�����ץ���������ٶ����°ڶ���������O�����·�ʱ�ſ����ӣ�������ñ�C���Զ�����жϲ���Ҫ˵�����ɣ�
���𰸡�
��1��
�⣺���Ӵ�A��B�������ɻ�е���غ㶨�ɵ�
mgL��1��cos60�㣩= ![]() mv2
mv2
v= ![]()
�������ݵ�
v=6m/s
��2��
�⣺����Ӿ���B��ʱ�ܵ����ӵ�������СΪFT����ţ�ٵڶ����ɵ�
FT��mg=m ![]()
��FT=mg+m ![]()
�������ݵ�
FT=100N
��3��
�⣺���Ӵ�B��C������ƽ���˶�
H��L= ![]() gt2
gt2
��t= ![]()
�������ݵ�
t=0.6s
��ص�C������O���ˮƽ����
x=vt
�������ݵ�
x=3.6m
��4��
�⣺����������������е���O��L1�����°ڶ�������O�����·�ʱ�ٶȼ�Ϊv1
mgL1��1��cos60�㣩= ![]() mv12
mv12
H��L1= ![]() gt12
gt12
��ص���O����ˮƽ����
x1=v1t1= ![]()
��õ�L1= ![]() H=2.7mʱ��Զ
H=2.7mʱ��Զ
��ˣ����ӿ�����ñ�C���Զ��
����������1���ɾ�ֹ�ͷţ�ϸ������������������е���غ㣬�ݴ˶�����ʽ����ú��Ӱڵ���͵�Bʱ���ٶȴ�С����2������͵㣬��������ϸ�������ĺ����ṩС���������������ţ�ٵڶ��������ϸ����������С����3��������B��ſ����Ӻ���ƽ���˶�����ƽ���˶��Ĺ�������ص�C������O���ˮƽ���룻��4��������ϵķ����������������������������һ���������ƽ���˶�ʱ��ˮƽ����λ�Ƶ����ֵ���ɣ�
�����㾫�����������⣬������Ҫ�˽�ƽ���˶�(�ص�:�پ���ˮƽ����ij��ٶ�;��ֻ���������ã��Ǽ��ٶ�Ϊ�������ٶ�g���ȱ��������˶����˶�����:ƽ���˶����Էֽ�Ϊˮƽ���������ֱ���˶�����ֱ��������������˶�)����Ҫ���ջ�е���غ㼰������(��ֻ���������͵��ɵ����������������£����嶯�ܺ��������ܣ����������ܣ������ת��������е�ܵ��������ֲ���)�����֪ʶ���Ǵ���Ĺؼ���

 ȫ�ŵ�����Ԫ�ƻ�ϵ�д�
ȫ�ŵ�����Ԫ�ƻ�ϵ�д�