Question

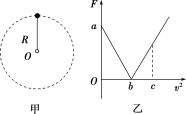
【题目】如图甲所示，轻杆一端固定在O点，另一端固定一小球，现让小球在竖直平面内做半径为R的圆周运动．小球运动到最高点时，杆与小球间弹力大小为F，小球在最高点的速度大小为v，其F－v2图象如图乙所示．则

A.小球的质量为

B.当地的重力加速度大小为

C.v2＝c时，小球对杆的弹力方向向上

D.v2＝2b时，小球受到的弹力与重力大小相等

Answer 1

【答案】ACD

【解析】

对小球在最高点进行受力分析，速度为零时：

F－mg＝0

结合图象可知

a－mg＝0

A．当F＝0时由牛顿第二定律可得：

结合图象可知：

联立解得，，选项A正确，B错误；

C．由图象可知b<c，当v2＝c时，根据牛顿第二定律有:

F＋mg＝

则杆对小球有向下的拉力，由牛顿第三定律可知，选项C正确；

D．当v2＝2b时，由牛顿第二定律可得:

mg＋F′＝

可得F′＝mg.选项D正确．