题目内容
3. 两极板M、N相距为d,板长为5d,两板未带电,板间有垂直于纸面的匀强磁场,如图所示,一大群电子沿平行于板的方向从各个位置以速度v射入板间,为了使电子都不从板间穿出,磁感应强度B的范围怎样?(设电子电荷量为e,质量为m)
两极板M、N相距为d,板长为5d,两板未带电,板间有垂直于纸面的匀强磁场,如图所示,一大群电子沿平行于板的方向从各个位置以速度v射入板间,为了使电子都不从板间穿出,磁感应强度B的范围怎样?(设电子电荷量为e,质量为m)
分析 由图可知电子向下偏转,则位于上极板的电子,打在下板的右边界时,轨道半径最大,磁场有最小值;打在下板的左边界,轨道半径最小,磁场有最大值.
解答 解:由图示可知,靠近M板进入磁场的电子刚好打到N板右边缘, 对应的磁感应强度有最小值B1,设此时轨道半径为R1,
对应的磁感应强度有最小值B1,设此时轨道半径为R1,
由牛顿第二定律得:evB1=m$\frac{{v}^{2}}{{R}_{1}}$,
由几何关系得(R1-d)2+(5d)2=R12,
解得:B1=$\frac{mv}{13ed}$;
靠近M板进入磁场的电子刚好打到N板左边缘,对应的磁感应强度有最大值B2,此时轨道半径为R2,
由牛顿第二定律:evB2=m$\frac{{v}^{2}}{{R}_{2}}$,
由几何关系得:R2=$\frac{d}{2}$,
解得:B2=$\frac{2mv}{ed}$,
综上所述,磁感应强度B的范围为:$\frac{mv}{13ed}$≤B≤$\frac{2mv}{ed}$;
答:为了使电子都不从板间穿出,磁感应强度B的范围是$\frac{mv}{13ed}$≤B≤$\frac{2mv}{ed}$.
点评 本题重点是对电子轨道的判定,即什么时候出现的是最小轨道,什么情况是最大轨道,对于这种求范围的问题,就是要抓住题目中给的限定条件,来找相关的物理量.

练习册系列答案
相关题目
11.-个物体做直线运动,其图象如图所示,以下说法正确的是( )


| A. | 前5s内的位移达到最大值 | |
| B. | 0-2s内物体的加速度为1.5m/s2 | |
| C. | 4-6s内物体的速度一直在减小 | |
| D. | 0<t<2s和5s<t<6s内加速度方向与速度方向相同 |
18.下列说法不正确的是( )
| A. | 三种起电方式中的摩擦起电不遵守电荷守恒定律 | |
| B. | 任何带电体的电荷量是元电荷的整数倍 | |
| C. | 点电荷和试探电荷都是一种理想模型 | |
| D. | 自然界只存在正电荷和负电荷,同种电荷相互吸引,异种电荷相互排斥 |
8.从高处静止释放一石块,石块做自由落体运动,已知他在第1秒内下落的高速是h,则它在第3秒内下落的高度是( )
| A. | 3h | B. | 5h | C. | 7h | D. | 9h |
15.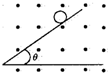 质量为m、带电量为q的小球,从倾角为θ的光滑绝缘斜面上由静止下滑,整个斜面置于方向水平向外的匀强磁场中,其磁感应强度为B,如图所示.若带电小球下滑后某时刻对斜面的作用力恰好为零,下面说法中正确的是( )
质量为m、带电量为q的小球,从倾角为θ的光滑绝缘斜面上由静止下滑,整个斜面置于方向水平向外的匀强磁场中,其磁感应强度为B,如图所示.若带电小球下滑后某时刻对斜面的作用力恰好为零,下面说法中正确的是( )
 质量为m、带电量为q的小球,从倾角为θ的光滑绝缘斜面上由静止下滑,整个斜面置于方向水平向外的匀强磁场中,其磁感应强度为B,如图所示.若带电小球下滑后某时刻对斜面的作用力恰好为零,下面说法中正确的是( )
质量为m、带电量为q的小球,从倾角为θ的光滑绝缘斜面上由静止下滑,整个斜面置于方向水平向外的匀强磁场中,其磁感应强度为B,如图所示.若带电小球下滑后某时刻对斜面的作用力恰好为零,下面说法中正确的是( )| A. | 小球带负电 | |
| B. | 小球在斜面上做匀加速直线运动 | |
| C. | 小球在斜面上做变加速直线运动 | |
| D. | 当小球对斜面压力为零时,其速率为$\frac{mgcosθ}{qB}$ |
12. 如图所示,倾角为θ的粗糙斜面上静止放置着一个质量为m的闭合正方形线框abcd,它与斜面间动摩擦因数为μ.线框边长为l,电阻为R.ab边紧靠宽度也为l的匀强磁场的下边界,磁感应强度为B,方向垂直于斜面向上.将线框用细线通过光滑定滑轮与重物相连,重物的质量为M,如果将线框和重物由静止释放,线框刚要穿出磁场时恰好匀速运动,重力加速度为g.下列说法正确的是( )
如图所示,倾角为θ的粗糙斜面上静止放置着一个质量为m的闭合正方形线框abcd,它与斜面间动摩擦因数为μ.线框边长为l,电阻为R.ab边紧靠宽度也为l的匀强磁场的下边界,磁感应强度为B,方向垂直于斜面向上.将线框用细线通过光滑定滑轮与重物相连,重物的质量为M,如果将线框和重物由静止释放,线框刚要穿出磁场时恰好匀速运动,重力加速度为g.下列说法正确的是( )
 如图所示,倾角为θ的粗糙斜面上静止放置着一个质量为m的闭合正方形线框abcd,它与斜面间动摩擦因数为μ.线框边长为l,电阻为R.ab边紧靠宽度也为l的匀强磁场的下边界,磁感应强度为B,方向垂直于斜面向上.将线框用细线通过光滑定滑轮与重物相连,重物的质量为M,如果将线框和重物由静止释放,线框刚要穿出磁场时恰好匀速运动,重力加速度为g.下列说法正确的是( )
如图所示,倾角为θ的粗糙斜面上静止放置着一个质量为m的闭合正方形线框abcd,它与斜面间动摩擦因数为μ.线框边长为l,电阻为R.ab边紧靠宽度也为l的匀强磁场的下边界,磁感应强度为B,方向垂直于斜面向上.将线框用细线通过光滑定滑轮与重物相连,重物的质量为M,如果将线框和重物由静止释放,线框刚要穿出磁场时恰好匀速运动,重力加速度为g.下列说法正确的是( )| A. | 线框刚开始运动时的加速度a=$\frac{Mg-mgsinθ-μmgcosθ}{m}$ | |
| B. | 线框匀速运动的速度v=$\frac{(Mg-mgsinθ-μmgcosθ)R}{{B}^{2}{l}^{2}}$ | |
| C. | 线框通过磁场过程中,克服摩擦力和安培力做的功等于线框机械能的减少量 | |
| D. | 线框通过磁场过程中,产生的焦耳热等于2(M-msinθ-μmcosθ)gl |
8. 如图光滑水平面上物块A和B以轻弹簧相连接.在水平拉力F作用下以加速度a作直线运动,设A和B的质量分别为mA和mB,当突然撤去外力F时( )
如图光滑水平面上物块A和B以轻弹簧相连接.在水平拉力F作用下以加速度a作直线运动,设A和B的质量分别为mA和mB,当突然撤去外力F时( )
 如图光滑水平面上物块A和B以轻弹簧相连接.在水平拉力F作用下以加速度a作直线运动,设A和B的质量分别为mA和mB,当突然撤去外力F时( )
如图光滑水平面上物块A和B以轻弹簧相连接.在水平拉力F作用下以加速度a作直线运动,设A和B的质量分别为mA和mB,当突然撤去外力F时( )| A. | 物块A的加速度为a | B. | 物块B的加速度为0 | ||
| C. | 物块A的加速度为$\frac{{m}_{A}a}{{m}_{A}+{m}_{B}}$ | D. | 物块B的加速度为-$\frac{{m}_{A}}{{m}_{B}}$a |
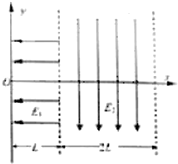 电学中有些仪器经常用到下述电子运动的物理原理.某一水平面内有一直角坐标系xOy平面,x=0和x=L=10cm的区间内有一沿x轴负方向的有理想边界的匀强电场E1=1.0×104V/m,x=L和x=3L的区间内有一沿y轴负方向的有理想边界的匀强电场E2=1.0×104V/m,一电子(为了计算简单,比荷取为$\frac{e}{m}$=1×1011C/kg)从直角坐标系xOy平面内的坐标原点O以很小的速度进入匀强电场E1,计算时不计此速度且只考虑xOy平面内的运动.求:
电学中有些仪器经常用到下述电子运动的物理原理.某一水平面内有一直角坐标系xOy平面,x=0和x=L=10cm的区间内有一沿x轴负方向的有理想边界的匀强电场E1=1.0×104V/m,x=L和x=3L的区间内有一沿y轴负方向的有理想边界的匀强电场E2=1.0×104V/m,一电子(为了计算简单,比荷取为$\frac{e}{m}$=1×1011C/kg)从直角坐标系xOy平面内的坐标原点O以很小的速度进入匀强电场E1,计算时不计此速度且只考虑xOy平面内的运动.求: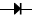 ”,其特点是具有单向导电性,即电流从正极流入时电阻比较小,而从负极流入时电阻很大.
”,其特点是具有单向导电性,即电流从正极流入时电阻比较小,而从负极流入时电阻很大.
