题目内容
如图所示,质量为m的飞行器在绕地球的圆轨道上运行,半径为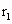 ,要进入半径为
,要进入半径为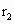 的更高的圆轨道Ⅱ,必须先加速进入一个椭圆轨Ⅲ,然后再进入圆轨道Ⅱ.已知飞行器在圆轨道Ⅱ上运动速度大小为v,在A点时通过发动机向后喷出一定质量气体使飞行器速度增加到
的更高的圆轨道Ⅱ,必须先加速进入一个椭圆轨Ⅲ,然后再进入圆轨道Ⅱ.已知飞行器在圆轨道Ⅱ上运动速度大小为v,在A点时通过发动机向后喷出一定质量气体使飞行器速度增加到 进入椭圆轨道Ⅲ,设喷出的气体的速度为u,求:
进入椭圆轨道Ⅲ,设喷出的气体的速度为u,求:
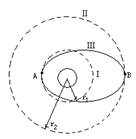
(1)飞行器在轨道Ⅰ上的速度 及轨道Ⅰ处的重力加速度;
及轨道Ⅰ处的重力加速度;
(2)飞行器喷出气体的质量;
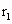 ,要进入半径为
,要进入半径为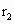 的更高的圆轨道Ⅱ,必须先加速进入一个椭圆轨Ⅲ,然后再进入圆轨道Ⅱ.已知飞行器在圆轨道Ⅱ上运动速度大小为v,在A点时通过发动机向后喷出一定质量气体使飞行器速度增加到
的更高的圆轨道Ⅱ,必须先加速进入一个椭圆轨Ⅲ,然后再进入圆轨道Ⅱ.已知飞行器在圆轨道Ⅱ上运动速度大小为v,在A点时通过发动机向后喷出一定质量气体使飞行器速度增加到 进入椭圆轨道Ⅲ,设喷出的气体的速度为u,求:
进入椭圆轨道Ⅲ,设喷出的气体的速度为u,求:
(1)飞行器在轨道Ⅰ上的速度
 及轨道Ⅰ处的重力加速度;
及轨道Ⅰ处的重力加速度;(2)飞行器喷出气体的质量;
(1) 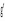 =
=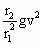 ·
·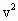 (2)
(2)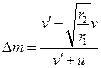
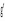 =
=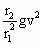 ·
·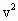 (2)
(2)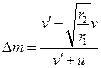
(1)在轨道I上,飞行器所受万有引力提供向心力,设地球质量为M,则有:
G·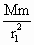 =m·
=m·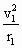
解得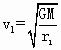
同理在轨道Ⅱ上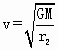
由①②可得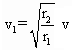
在轨道I上重力加速度为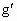 ,则有G·
,则有G·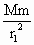 =
=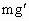
由③⑤可得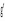 =
=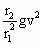 ·
·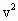
(2)设喷出气体质量为Δm,由动量守恒得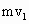 =(m-Δm)
=(m-Δm) -Δm·u,
-Δm·u,
解得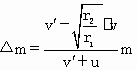
G·
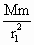 =m·
=m·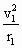
解得
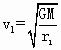
同理在轨道Ⅱ上
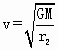
由①②可得
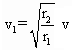
在轨道I上重力加速度为
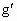 ,则有G·
,则有G·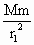 =
=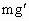
由③⑤可得
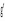 =
=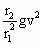 ·
·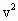
(2)设喷出气体质量为Δm,由动量守恒得
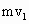 =(m-Δm)
=(m-Δm) -Δm·u,
-Δm·u,解得
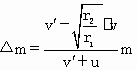

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目