题目内容
2.如图甲所示,竖直面MN的左侧空间中存在竖直向上的匀强电场(上、下及左侧无边界).一个质量为m、电荷量为q,可视为质点的带正电小球,以水平初速度v0沿PQ向右做直线运动.若小球刚经过D点时(t=0),在电场所在空间叠加如图乙所示随时间周期性变化、垂直纸面向里的匀强磁场,使得小球再次通过D点时与PQ连线成60°角.已知D、Q间的距离为($\sqrt{3}$+1)L,t0小于小球在磁场中做圆周运动的周期,忽略磁场变化造成的影响,重力加速度为g.求:
(1)电场强度E的大小;
(2)t0与t1的比值;
(3)小球过D点后将做周期性运动.则当小球运动的周期最大时,求出此时的磁感应强度B0及运动的最大周期Tm的大小,并在图中画出此情形下小球运动一个周期的轨迹.
分析 (1)根据电场力与重力,二力平衡,即可求解;
(2)根据小球做匀速圆周运动的周期与半径公式,结合几何关系,即可求解;
(3)根据几何关系,由牛顿第二定律,即可求解.
解答 解:(1)小球在电场中做匀速直线运动,根据二力平衡,则有:mg=qE;
解得:E=$\frac{mg}{q}$;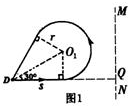
(2)小球能再次通过D点,其运动轨迹如图1所示,设圆弧半径为r;
则有:s=v0t;
由几何关系,有s=$\frac{r}{tan30°}$;
设小球做圆周运动的周期为T,则:T=$\frac{2πr}{{v}_{0}}$;
t0=$\frac{2}{3}T$;
由以上式联立可解得:$\frac{{t}_{0}}{{t}_{1}}=\frac{4\sqrt{3}}{9}π$;
(3)当小球运动的周期最大时,其运动轨迹应与MN相切,如图2所示,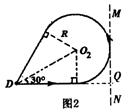
由几何关系,则有:R+$\frac{R}{tan30°}=(\sqrt{3}+1)L$;
由牛顿第二定律,则有:qv0B=m$\frac{{v}^{2}}{R}$;
解得:B0=$\frac{m{v}_{0}}{qL}$;
最大周期 ${T}_{m}=\frac{s}{{v}_{0}}=\frac{(4π+6\sqrt{3})L}{{v}_{0}}$
小球运动一个周期的轨迹,如图3所示,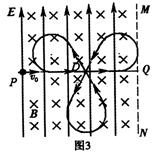
答:(1)电场强度E的大小$\frac{mg}{q}$;
(2)t0与t1的比值:$\frac{{t}_{0}}{{t}_{1}}=\frac{4\sqrt{3}}{9}π$;
(3)小球过D点后将做周期性运动.则当小球运动的周期最大时,求出此时的磁感应强度B0的大小B0=$\frac{m{v}_{0}}{qL}$;运动的最大周期Tm的大小$\frac{(4π+6\sqrt{3})L}{{v}_{0}}$,小球运动一个周期的轨迹如上图所示.
点评 考查粒子做匀速圆周运动,洛伦兹力提供向心力,掌握牛顿第二定律的应用,注意几何关系的正确建立,理解二力平衡条件.

 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案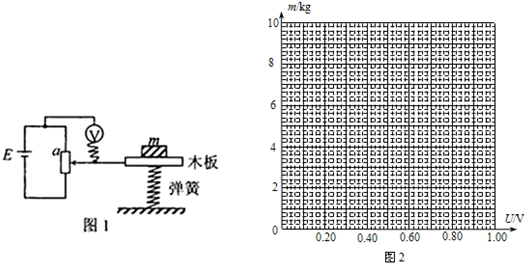
(1)写出m、U与k之间所满足的关系式.$m=\frac{lk}{Eg}U$
(2)己知E=1.50V,l=12.0cm,g=9.80m/s2.测量结果如表:
| m(kg) | 1.00 | 1.50 | 3.00 | 4.50 | 6.00 | 7.50 |
| U(V) | 0.108 | 0.154 | 0.290 | 0.446 | 0.608 | 0.740 |
②m-U直线的斜率为10.0kg/V.
③弹簧的劲度系数k=1.24×103N/m.(保留3位有效数字)
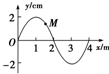 沿x轴正向传播的一列简谐横波在t=0时刻的波形如图所示,M为介质中的一个质点,该波的传播速度为40m/s,则t=$\frac{1}{40}$s时( )
沿x轴正向传播的一列简谐横波在t=0时刻的波形如图所示,M为介质中的一个质点,该波的传播速度为40m/s,则t=$\frac{1}{40}$s时( )| A. | 质点M对平衡位置的位移一定为负值 | |
| B. | 质点M的速度方向与对平衡位置的位移方向相同 | |
| C. | 质点M的加速度方向与速度方向一定相同 | |
| D. | 质点M的回复力方向与对平衡位置的位移方向相同 |
 如图所示为表演“杂技飞车走壁”的示意图,演员骑摩托车在一个锥形圆桶结构的内壁上飞驰,做匀速圆周运动,图中a、b两个虚线圆表示同一位演员骑同一辆摩托车,在离地面不同高度处进行表演的运动轨迹.不考虑车轮受到的侧向摩擦,下列说法中正确的是( )
如图所示为表演“杂技飞车走壁”的示意图,演员骑摩托车在一个锥形圆桶结构的内壁上飞驰,做匀速圆周运动,图中a、b两个虚线圆表示同一位演员骑同一辆摩托车,在离地面不同高度处进行表演的运动轨迹.不考虑车轮受到的侧向摩擦,下列说法中正确的是( )| A. | 在b轨道上运动时角速度较大 | |
| B. | 在b轨道上运动时线速度较大 | |
| C. | 在b轨道上运动时摩托车对侧壁的压力较小 | |
| D. | 在b轨道上运动时摩托车和运动员所需的向心力较小 |
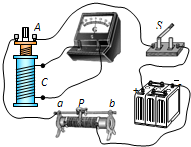 “研究感应电流产生的条件”的实验电路如图所示.实验表明:当穿过闭合电路的磁通量发生变化时,闭合电路中就会有电流产生.在闭合电键S前,滑动变阻器滑动片P应置于a端(选填“a”或“b”).电键S闭合后还有多种方法能使线圈C中产生感应电流.
“研究感应电流产生的条件”的实验电路如图所示.实验表明:当穿过闭合电路的磁通量发生变化时,闭合电路中就会有电流产生.在闭合电键S前,滑动变阻器滑动片P应置于a端(选填“a”或“b”).电键S闭合后还有多种方法能使线圈C中产生感应电流.
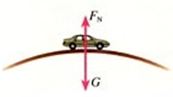 一辆质量为800kg的小汽车驶上圆弧半径为50m的拱桥.
一辆质量为800kg的小汽车驶上圆弧半径为50m的拱桥.