Question

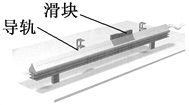
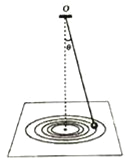
【题目】某同学用圆锥摆粗略验证向心力的表达式Fn=mrω2，实验装罝如图所示．细线下悬挂一个钢球，上端固定在铁架台上，将画着几个同心圆的白纸置于水平桌面上，使钢球静止时正好位于圆心处，与白纸接触但无挤压．用手带动钢球，设法使它沿纸面上某个圆做圆周运动．测得钢球质量m=0.100kg，转动的圆周半径为3.30cm，细线悬点与白纸上圆心的距离d=1.10m，当地重力加速度g=9.8m/s2．（计箅结果保留三位有效数字）

（1）图中细线与竖直方向的夹角θ比较小，可认为tanθ≈sinθ，其中sinθ=_____；依据受力分析，钢球做匀速圆周运动时所受的合外力F1=________N；

（2）用秒表测得圆锥摆运动30圈的总时间为t=62.5s，则该圆周运动周期T=______s，再利用向心力的表达式Fn=mrω2可以得到钢球运动的向心力F2 =_______N．

（3）在误差允许的范围内，可认为F1_______F2（填“=”、“＞”、“＜”），证明向心力的表达式是正确的．

Answer 1

【答案】 3.00×10﹣2 2.94×10﹣2 2.08 3.00×10﹣2 =

【解析】（1）根据几何关系知， ，根据平行四边形定则知，钢球所受的合外力．
（2）圆锥摆的周期，

向心力．
（3）在误差允许的范围内，可认为，证明向心力的表达式是正确的。