题目内容
 如图所示,轻绳的一端系一小球,另一端固定于O点,在O点的正下方P点钉颗一钉子,使悬线拉紧与竖直方向成一角度θ,然后由静止释放小球,当悬线碰到钉子时( )
如图所示,轻绳的一端系一小球,另一端固定于O点,在O点的正下方P点钉颗一钉子,使悬线拉紧与竖直方向成一角度θ,然后由静止释放小球,当悬线碰到钉子时( )分析:由机械能守恒可知小球到达最低点的速度,小球碰到钉子后仍做圆周运动,由向心力公式可得出绳子的拉力与小球转动半径的关系;由圆周运动的性质可知其线速度、角速度及向心加速度的大小关系.
解答:解:A.小球摆下后由机械能守恒可知,mgh=
mv2,因小球下降的高度相同,故小球到达最低点时的速度相同,故小球的线速度不变,故A错误;
B.根据ω=
,v不变,r变小,故ω变大,故B错误;
C.设钉子到球的距离为R,则F-mg=m
,故绳子的拉力F=mg+m
因R小于L,故有钉子时,绳子上的拉力变大,故C错误;
D.小球的向心加速度a=
,R<L,故小球的向心加速度增大,故D正确.
故选D.
| 1 |
| 2 |
B.根据ω=
| v |
| r |
C.设钉子到球的距离为R,则F-mg=m
| v2 |
| R |
| v2 |
| R |
D.小球的向心加速度a=
| v2 |
| R |
故选D.
点评:本题中要注意细绳碰到钉子前后转动半径的变化,再由向心力公式分析绳子上的拉力变化.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
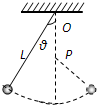 如图所示,轻绳的一端系一小球,另一端固定于O点,在O点的正下方P点钉颗一钉子,使悬线拉紧与竖直方向成一角度θ,然后由静止释放小球,当悬线碰到钉子时( )
如图所示,轻绳的一端系一小球,另一端固定于O点,在O点的正下方P点钉颗一钉子,使悬线拉紧与竖直方向成一角度θ,然后由静止释放小球,当悬线碰到钉子时( )| A、小球的瞬时速度突然变大 | B、小球的角速度突然变大 | C、绳上拉力突然变小 | D、球的加速度突然变小 |
 (2010?湘潭一模)如图所示,轻绳的一端固定在竖直墙上,另一端系一质量m=1kg的金属球,球与墙之间挤压一个轻弹簧,当金属球静止时弹簧水平,轻绳与竖直墙壁之间的夹角为60°;则剪断轻细绳的瞬间,金属球的加速度大小为( )
(2010?湘潭一模)如图所示,轻绳的一端固定在竖直墙上,另一端系一质量m=1kg的金属球,球与墙之间挤压一个轻弹簧,当金属球静止时弹簧水平,轻绳与竖直墙壁之间的夹角为60°;则剪断轻细绳的瞬间,金属球的加速度大小为( ) 如图所示,轻绳的一端固定在O点,另一端系一质量为m的小球(可视为质点).当小球在竖直平面内沿逆时针方向做圆周运动时,通过传感器测得轻绳拉力T、轻绳与竖直线OP的夹角θ满足关系式T=a+bcosθ,式中a、b为常数.若不计空气阻力,则当地的重力加速度为( )
如图所示,轻绳的一端固定在O点,另一端系一质量为m的小球(可视为质点).当小球在竖直平面内沿逆时针方向做圆周运动时,通过传感器测得轻绳拉力T、轻绳与竖直线OP的夹角θ满足关系式T=a+bcosθ,式中a、b为常数.若不计空气阻力,则当地的重力加速度为( ) 如图所示,轻绳的一端悬挂在天花板上,另一端系一质量为m的光滑小球,小球与质量为M的斜面体相接触,已知斜面体受到水平向左的推力F,小球和斜面体处于静止状轻绳沿竖直方向,重力加速度为g,则下列说法正确的是( )
如图所示,轻绳的一端悬挂在天花板上,另一端系一质量为m的光滑小球,小球与质量为M的斜面体相接触,已知斜面体受到水平向左的推力F,小球和斜面体处于静止状轻绳沿竖直方向,重力加速度为g,则下列说法正确的是( )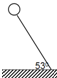 如图所示,轻绳的一端系在地上,另一端系着氢气球,氢气球重20N,空气对它的浮力恒为30N,由于受恒定水平风力作用,使系氢气球的轻绳和地面成53°角,(g取10m/s2)则:
如图所示,轻绳的一端系在地上,另一端系着氢气球,氢气球重20N,空气对它的浮力恒为30N,由于受恒定水平风力作用,使系氢气球的轻绳和地面成53°角,(g取10m/s2)则: