Question

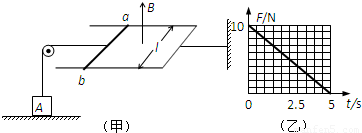
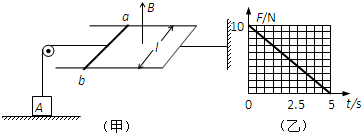如图（甲）所示，“U”型金属导轨水平放置，右端固定，导体棒ab与导轨的两臂垂直放置，ab与导轨构成边长l=1.0m的正方形，整个回路的电阻R=2Ω．质量m=1kg的物体A置于水平地面上，通过轻绳绕过定滑轮与导体棒ab相连，当垂直于导轨平面向上的磁场按B=kt（k为恒量）均匀增大时，物体A对地面的压力F随时间t变化的图象如图（乙）所示．不考虑一切阻力，取g=10m/s²．求：
（1）k值；
（2）导体棒ab中感应电流的大小和方向；
（3）在0-5s时间内回路中产生的焦耳热．

Answer 1

分析：（1）根据法拉第电磁感应定律、欧姆定律、安培力公式联立求解出安培力的表达式，然后结合图象中数据求解出k值；
（2）根据法拉第电磁感应定律、欧姆定律列式求解出电流，根据右手定则判断安培力方向；
（3）根据焦耳定律直接列式求解焦耳热．

解答：解：（1）设回路中产生的感应电动势为E，根据法拉第电磁感应定律有：E=

△Φ

△t

其中△Φ=△BS=△Bl²
根据题意有：k=

△B

△t

设回路中的感应电流为I，根据闭合电路欧姆定律有：I=

E

R

设导体棒ab所受的安培力为F，根据安培力公式有：F=IlB
联立解得：F=

k2l3

R

t
由图象可知，t=5s时，安培力大小等于A的重力10 N，即：

k2l3

R

t=10
解得：k=2T/s
（2）回路中的感应电流大小为：I=

E

R

=

kl2

R

=1A
根据楞次定律知，感应电流方向由b指向a．
（3）根据焦耳定律，在0-5s时间内回路中产生的焦耳热为：Q=I²Rt=10J．
答：（1）k值为2T/s；
（2）导体棒ab中感应电流的大小为1A，方向为由b指向a；
（3）在0-5s时间内回路中产生的焦耳热为10J．

点评：本题关键是根据法拉第电磁感应定律、欧姆定律和安培力公式列式求解出安培力的一般表达式进行讨论，然后结合右手定则、焦耳定律列式分析．