题目内容
13.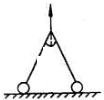 如图所示,两个完全相同的小球,质量均为m,两球与水平地面间的动摩擦因数都为μ,且假设最大静摩擦力等于滑动摩擦力,一根轻绳两端固结在两个球上,在绳的中间施加一个竖直向上的拉力,绳被拉直后,中点与绳延长线过球心,绳与水平方向夹角为α.
如图所示,两个完全相同的小球,质量均为m,两球与水平地面间的动摩擦因数都为μ,且假设最大静摩擦力等于滑动摩擦力,一根轻绳两端固结在两个球上,在绳的中间施加一个竖直向上的拉力,绳被拉直后,中点与绳延长线过球心,绳与水平方向夹角为α.(1)当用F1拉绳且两球静止时,绳的拉力多大?地面与球之间的弹力多大?
(2)竖直向上的拉力为多大时,两球将发生滑动.
分析 (1)对结点O和左边一个小球,受力分析,画出受力分析图,根据平衡条件列式即可求解;
(2)当用力拉绳子的中点时,绳子对两球有作用力,使它们要发生滑动.则对球受力分析由力的合成,得出两段绳间的夹角为α时绳子力大小,从而再对O点进行受力分析,再由力的合成去寻找力的三角函数关系.
解答 解:对结点O和左边一个小球,受力分析,如图所示,
根据平衡条件得:
Tcos(90°-α)=$\frac{{F}_{1}}{2}$
解得:T=$\frac{{F}_{1}}{2sinα}$
N+Tsinα=mg
解得:N=$mg-\frac{{F}_{1}}{2}$
(2)对任一球(如右球),受力分析,如图所示:
球发生滑动的临界条件是:
F2cosα=μFN.
又F2sinα+FN=mg.
解得:F2=$\frac{μmg}{cosα+μsinα}$,
则F=2F2sinα=$\frac{2μmgsinα}{cosα+μsinα}$
答:(1)当用F1拉绳且两球静止时,绳的拉力为$\frac{{F}_{1}sinα}{2}$,地面与球之间的弹力为$mg-\frac{{F}_{1}}{2}$;
(2)竖直向上的拉力为$\frac{2μmgsinα}{cosα+μsinα}$时,两球将发生滑动.
点评 本题主要考查了共点力平衡条件的直接应用,要求同学们能正确对物体进行受力分析,在进行力处理时,三个力构成的三角形有的是构成直角三角形,有的是构成等腰三角形,有的是构成等边三角形.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
3. 如图所示,均匀介质中两波源S1、S2分别位于x轴上的x1=0、x2=16m处,质点P位于x轴上的x3=4m处.t=0时刻,两波源同时由平衡位置开始向上振动,振动周期T=0.1s,传播速度均为v=80m/s.波源S1的振幅A1=3cm,波源S2的振幅A2=4cm.则从t=0到t=0.35s时间内质点P通过的路程为( )
如图所示,均匀介质中两波源S1、S2分别位于x轴上的x1=0、x2=16m处,质点P位于x轴上的x3=4m处.t=0时刻,两波源同时由平衡位置开始向上振动,振动周期T=0.1s,传播速度均为v=80m/s.波源S1的振幅A1=3cm,波源S2的振幅A2=4cm.则从t=0到t=0.35s时间内质点P通过的路程为( )
 如图所示,均匀介质中两波源S1、S2分别位于x轴上的x1=0、x2=16m处,质点P位于x轴上的x3=4m处.t=0时刻,两波源同时由平衡位置开始向上振动,振动周期T=0.1s,传播速度均为v=80m/s.波源S1的振幅A1=3cm,波源S2的振幅A2=4cm.则从t=0到t=0.35s时间内质点P通过的路程为( )
如图所示,均匀介质中两波源S1、S2分别位于x轴上的x1=0、x2=16m处,质点P位于x轴上的x3=4m处.t=0时刻,两波源同时由平衡位置开始向上振动,振动周期T=0.1s,传播速度均为v=80m/s.波源S1的振幅A1=3cm,波源S2的振幅A2=4cm.则从t=0到t=0.35s时间内质点P通过的路程为( )| A. | 98cm | B. | 14cm | C. | 56cm | D. | 68cm |
4. 如图所示,在倾角为α=30°的光滑固定斜面上,有两个质量均为m的小球A、B,它们用劲度系数为k的轻弹簧连接,相对A施加一水平向右的恒力,使A、B均静止在斜面上,此时弹簧的长度为L,下列说法正确的是( )
如图所示,在倾角为α=30°的光滑固定斜面上,有两个质量均为m的小球A、B,它们用劲度系数为k的轻弹簧连接,相对A施加一水平向右的恒力,使A、B均静止在斜面上,此时弹簧的长度为L,下列说法正确的是( )
 如图所示,在倾角为α=30°的光滑固定斜面上,有两个质量均为m的小球A、B,它们用劲度系数为k的轻弹簧连接,相对A施加一水平向右的恒力,使A、B均静止在斜面上,此时弹簧的长度为L,下列说法正确的是( )
如图所示,在倾角为α=30°的光滑固定斜面上,有两个质量均为m的小球A、B,它们用劲度系数为k的轻弹簧连接,相对A施加一水平向右的恒力,使A、B均静止在斜面上,此时弹簧的长度为L,下列说法正确的是( )| A. | 弹簧的原长为L-$\frac{mg}{2k}$ | |
| B. | 水平恒力大小为$\frac{2\sqrt{3}}{3}$mg | |
| C. | 撤掉恒力的瞬间小球A的加速度为$\frac{g}{2}$ | |
| D. | 撤掉恒力的瞬间小球B的加速度为0 |
8.将一段确定的导线做成线圈,在确定的匀强磁场中绕垂直于磁场的轴线以固定的转速转动,产生的交流电动势最大的情况是( )
| A. | 做成方形线圈,线圈平面垂直于转轴 | |
| B. | 做成方形线圈,转轴通过线圈平面 | |
| C. | 做成圆形线圈,转轴通过线圈平面 | |
| D. | 做成任意形状,只要转轴通过线圈平面 |
7. 如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感应强度为B.有一质量为m,长为L导体棒从ab位置获得平行于斜面的、大小为v的初速度向上运动,最远到达cd的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ,则( )
如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感应强度为B.有一质量为m,长为L导体棒从ab位置获得平行于斜面的、大小为v的初速度向上运动,最远到达cd的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ,则( )
 如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感应强度为B.有一质量为m,长为L导体棒从ab位置获得平行于斜面的、大小为v的初速度向上运动,最远到达cd的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ,则( )
如图所示,平行金属导轨与水平面间的倾角为θ,导轨电阻不计,与阻值为R的定值电阻相连,匀强磁场垂直穿过导轨平面,磁感应强度为B.有一质量为m,长为L导体棒从ab位置获得平行于斜面的、大小为v的初速度向上运动,最远到达cd的位置,滑行的距离为s,导体棒的电阻也为R,与导轨之间的动摩擦因数为μ,则( )| A. | 上滑动过程中电流做功发出的热量为$\frac{1}{2}$mv2-mgs(sinθ+μcosθ) | |
| B. | 上滑动过程中导体棒做匀减速直线运动 | |
| C. | 上滑动过程中导体棒损失的机械能为$\frac{1}{2}$mv2 | |
| D. | 上滑动过程中导体棒受到的最大安培力为$\frac{{B}^{2}{L}^{2}v}{R}$ |
 如图所示,用细线OC的一端将质量m=1kg的物体系住,另一端用细线AO,BO结在一起,O为结点,A端系在竖直墙壁间上,与墙壁间的夹角为30°,B端与另一个质量M=10kg的物体相连,M放在倾角为30°的粗糙斜面上,OB与斜面平行,整个系统处于静止状态,最大静摩擦力可认为与滑动摩擦力相等,当地的重力加速度g=10m/s2,求:
如图所示,用细线OC的一端将质量m=1kg的物体系住,另一端用细线AO,BO结在一起,O为结点,A端系在竖直墙壁间上,与墙壁间的夹角为30°,B端与另一个质量M=10kg的物体相连,M放在倾角为30°的粗糙斜面上,OB与斜面平行,整个系统处于静止状态,最大静摩擦力可认为与滑动摩擦力相等,当地的重力加速度g=10m/s2,求:
 如图所示的平行板器件中,存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1=0.40T,方向垂直纸面向里,电场强度E=2.0×105V/m,PQ为板间中线.紧靠平行板右侧边缘xOy坐标系的第一象限内,有垂直纸面向外的匀强磁场,磁感应强度B2=0.25T,磁场边界AO和y轴的夹角∠AOy=45°.一束带电量q=8.0×10-19C的正离子从P点射入平行板间,沿中线PQ做直线运动,穿出平行板后从y轴上坐标为(0,0.2m)的Q点垂直y轴射入磁场区,离子通过x轴时的速度方向与x轴正方向夹角在45°~90°之间.则:
如图所示的平行板器件中,存在相互垂直的匀强磁场和匀强电场,磁场的磁感应强度B1=0.40T,方向垂直纸面向里,电场强度E=2.0×105V/m,PQ为板间中线.紧靠平行板右侧边缘xOy坐标系的第一象限内,有垂直纸面向外的匀强磁场,磁感应强度B2=0.25T,磁场边界AO和y轴的夹角∠AOy=45°.一束带电量q=8.0×10-19C的正离子从P点射入平行板间,沿中线PQ做直线运动,穿出平行板后从y轴上坐标为(0,0.2m)的Q点垂直y轴射入磁场区,离子通过x轴时的速度方向与x轴正方向夹角在45°~90°之间.则: 在“测定金属的电阻率”的实验中:
在“测定金属的电阻率”的实验中: