题目内容
20. 如图,在足够长的光滑水平面上,物体A、B、C位于同一直线上,A点位于B、C之间,A的质量为m,B、C的质量都为M,三者均处于静止状态,现使A以某一速度向右运动,求m和M之间应满足什么条件,才能使A只与B、C各发生一次碰撞.设物体间的碰撞都是弹性的.
如图,在足够长的光滑水平面上,物体A、B、C位于同一直线上,A点位于B、C之间,A的质量为m,B、C的质量都为M,三者均处于静止状态,现使A以某一速度向右运动,求m和M之间应满足什么条件,才能使A只与B、C各发生一次碰撞.设物体间的碰撞都是弹性的.
分析 该题中A与C的碰撞过程以及A与B的碰撞的过程都是弹性碰撞,将动量守恒定律与机械能守恒定律相结合即可正确解答.
解答 解:A向右运动与C发生碰撞的过程中系统的动量守恒、机械能守恒,选取向右为正方向,设开始时A的速度为v0,第一次与C碰撞后C的速度为vC1,A的速度为vA1.由动量守恒定律、机械能守恒定律得:
mv0=mvA1+MvC1 ①
$\frac{1}{2}m{v}_{0}^{2}=\frac{1}{2}m{v}_{A1}^{2}+\frac{1}{2}M{v}_{C1}^{2}$ ②
联立①②得:vA1=$\frac{m-M}{m+M}{v}_{0}$ ③
vC1=$\frac{2m}{m+M}{v}_{0}$ ④
可知,只有m<M时,A才能被反向弹回,才可能与B发生碰撞.
A与B碰撞后B的速度为vB1,A的速度为vA2.由动量守恒定律、机械能守恒定律,同理可得:
vA2=$\frac{m-M}{m+M}{v}_{A1}$=$(\frac{m-M}{m+M})^{2}{v}_{0}$ ⑤
根据题意要求A只与B、C各发生一次碰撞,应有:vA2≤vC1 ⑥
联立④⑤⑥得:m2+4mM-M2≥0
解得:$m≥(\sqrt{5}-2)M$,(另一解:$m≤-(\sqrt{5}+2)M$舍去)所以m与M之间的关系应满足:
$M>m≥(\sqrt{5}-2)M$
答:m和M之间应满足$M>m≥(\sqrt{5}-2)M$,才能使A只与B、C各发生一次碰撞.
点评 本题考查了水平方向的动量守恒定律问题,分析清楚物体运动过程、应用动量守恒定律、能量守恒定律即可正确解题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11. 如图所示,一束单色光从空气入射到棱镜的AB面上,经AB和AC两个面折射后从AC面进入空气,当出射角i′和入射角i相等时,出射光线相对于入射光线偏转的角度为θ,已知棱镜顶角为α,则计算棱镜对该色光的折射率表达式为( )
如图所示,一束单色光从空气入射到棱镜的AB面上,经AB和AC两个面折射后从AC面进入空气,当出射角i′和入射角i相等时,出射光线相对于入射光线偏转的角度为θ,已知棱镜顶角为α,则计算棱镜对该色光的折射率表达式为( )
 如图所示,一束单色光从空气入射到棱镜的AB面上,经AB和AC两个面折射后从AC面进入空气,当出射角i′和入射角i相等时,出射光线相对于入射光线偏转的角度为θ,已知棱镜顶角为α,则计算棱镜对该色光的折射率表达式为( )
如图所示,一束单色光从空气入射到棱镜的AB面上,经AB和AC两个面折射后从AC面进入空气,当出射角i′和入射角i相等时,出射光线相对于入射光线偏转的角度为θ,已知棱镜顶角为α,则计算棱镜对该色光的折射率表达式为( )| A. | $\frac{sin\frac{α+θ}{2}}{sin\frac{α}{2}}$ | B. | $\frac{sin\frac{α+θ}{2}}{sin\frac{θ}{2}}$ | C. | $\frac{sinθ}{sin(θ-\frac{α}{2})}$ | D. | $\frac{sinα}{sin(α-\frac{θ}{2})}$ |
8. 一带有乒乓球发射机的乒乓球台如图所示,水平台面的长和宽分别为L1和L2,中间球网高度为h,发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h,不计空气的作用,重力加速度大小为g,若乒乓球的发射率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,到v的最大取值范围是( )
一带有乒乓球发射机的乒乓球台如图所示,水平台面的长和宽分别为L1和L2,中间球网高度为h,发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h,不计空气的作用,重力加速度大小为g,若乒乓球的发射率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,到v的最大取值范围是( )
 一带有乒乓球发射机的乒乓球台如图所示,水平台面的长和宽分别为L1和L2,中间球网高度为h,发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h,不计空气的作用,重力加速度大小为g,若乒乓球的发射率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,到v的最大取值范围是( )
一带有乒乓球发射机的乒乓球台如图所示,水平台面的长和宽分别为L1和L2,中间球网高度为h,发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h,不计空气的作用,重力加速度大小为g,若乒乓球的发射率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,到v的最大取值范围是( )| A. | $\frac{{L}_{1}}{2}$$\sqrt{\frac{g}{6h}}$<v<L1$\sqrt{\frac{g}{6h}}$ | B. | $\frac{{L}_{1}}{4}$$\sqrt{\frac{g}{h}}$<v<$\sqrt{\frac{(4{L}_{1}^{2}+{L}_{2}^{2})g}{6h}}$ | ||
| C. | $\frac{{L}_{1}}{2}$$\sqrt{\frac{g}{6h}}$<v<$\frac{1}{2}$$\sqrt{\frac{(4{L}_{1}^{2}+{L}_{2}^{2})g}{6h}}$ | D. | $\frac{{L}_{1}}{4}$$\sqrt{\frac{g}{h}}$<v<$\frac{1}{2}$$\sqrt{\frac{(4{L}_{1}^{2}+{L}_{2}^{2})g}{6h}}$ |
15.下列说法正确的是( )
| A. | 将一块晶体敲碎后,得到的小颗粒是非晶体 | |
| B. | 固体可以分为晶体和非晶体两类,有些晶体在不同方向上有不同的光学性质 | |
| C. | 由同种元素构成的固体,可能会由于原子的排列方式不同而成为不同的晶体 | |
| D. | 在合适的条件下,某些晶体可以转变为非晶体,某些非晶体也可以转变为晶体 | |
| E. | 在熔化过程中,晶体要吸收热量,但温度保持不变,内能也保持不变 |
5.某同学利用图(a)所示电路测量电容器充电时两极板间的电压随时间的变化.实验中使用的器材为:电池E(内阻很小)、开关S1和S2、电容器C(约100μF)、电阻R1(约200kΩ)、电阻R2(1kΩ)、电压表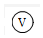 (量程6V)、秒表、导线若干.
(量程6V)、秒表、导线若干.
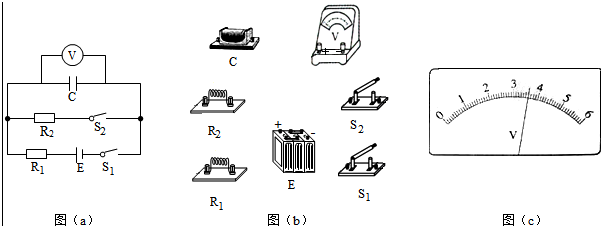
(1)按图(a)所示的电路原理图将图(b)中实物图连线.
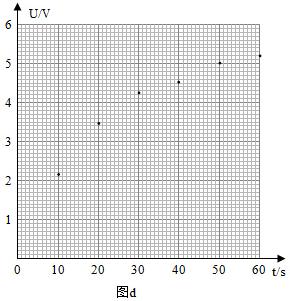
(2)先闭合开关S2,再断开开关S2;闭合开关S1,同时按下秒表开始计时,若某时刻电压表的示数如图(c)所示,电压表的读数为3.60V(保留2位小数).
(3)该同学每隔10s记录一次电压表的读数U,记录的数据如表所示,在图(d)给出的坐标纸上绘出U-t图线.已知只有一个数据点误差较大,该数据点对应的表中的时间是40s.
(4)电路中C、R2和S2构成的回路的作用是使实验前电容器两个极板上的电荷相中和.
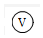 (量程6V)、秒表、导线若干.
(量程6V)、秒表、导线若干.
(1)按图(a)所示的电路原理图将图(b)中实物图连线.
(2)先闭合开关S2,再断开开关S2;闭合开关S1,同时按下秒表开始计时,若某时刻电压表的示数如图(c)所示,电压表的读数为3.60V(保留2位小数).
(3)该同学每隔10s记录一次电压表的读数U,记录的数据如表所示,在图(d)给出的坐标纸上绘出U-t图线.已知只有一个数据点误差较大,该数据点对应的表中的时间是40s.
| 时间t/s | 10.0 | 20.0 | 30.0 | 40.0 | 50.0 | 60.0 |
| 电压U/V | 2.14 | 3.45 | 4.23 | 4.51 | 5.00 | 5.18 |

(4)电路中C、R2和S2构成的回路的作用是使实验前电容器两个极板上的电荷相中和.
12.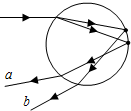 中国古人对许多自然现象有深刻认识,唐人张志和在《玄真子•涛之灵》中写道:“雨色映日而为虹”.从物理学角度看,虹是太阳光经过雨滴的两次折射和一次反射形成的.如图是彩虹成因的简化示意图,其中a、b是两种不同频率的单色光,则两光( )
中国古人对许多自然现象有深刻认识,唐人张志和在《玄真子•涛之灵》中写道:“雨色映日而为虹”.从物理学角度看,虹是太阳光经过雨滴的两次折射和一次反射形成的.如图是彩虹成因的简化示意图,其中a、b是两种不同频率的单色光,则两光( )
 中国古人对许多自然现象有深刻认识,唐人张志和在《玄真子•涛之灵》中写道:“雨色映日而为虹”.从物理学角度看,虹是太阳光经过雨滴的两次折射和一次反射形成的.如图是彩虹成因的简化示意图,其中a、b是两种不同频率的单色光,则两光( )
中国古人对许多自然现象有深刻认识,唐人张志和在《玄真子•涛之灵》中写道:“雨色映日而为虹”.从物理学角度看,虹是太阳光经过雨滴的两次折射和一次反射形成的.如图是彩虹成因的简化示意图,其中a、b是两种不同频率的单色光,则两光( )| A. | 在同种玻璃中传播,a光的传播速度一定大于b光 | |
| B. | 以相同角度斜射到同一玻璃板透过平行表面后,b光侧移量大 | |
| C. | 分别照射同一光电管,若b光能引起光电效应,a光也一定能 | |
| D. | 以相同的入射角从水中射入空气,在空气中只能看到一种光时,一定是a光 |
9.我国科学家正在研制航母舰载机使用的电磁弹射器,舰载机总质量为3.0×104kg,设起飞过程中发动机的推力恒为1.0×105N,弹射器有效作用长度为100m,推力恒定,要求舰载机在水平弹射结束时速度大小达到80m/s.弹射过程中舰载机所受总推力为弹射器和发动机推力之和,假设所受阻力为总推力的20%,则( )
| A. | 弹射器的推力大小为1.1×106N | |
| B. | 弹射器对舰载机所做的功为1.1×108J | |
| C. | 弹射器对舰载机做功的平均功率为8.8×107W | |
| D. | 舰载机在弹射过程中的加速度大小为32m/s2 |
10.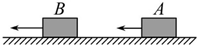 如图所示,A、B两小物块在光滑水平面上沿同一直线同向运动,动量分别为pA=6.0kg•m/s,pB=8.0kg•m/s.A追上B并与B相碰,碰后A、B的动量分别为pA′和pB′,pA′、pB′的值可能为( )
如图所示,A、B两小物块在光滑水平面上沿同一直线同向运动,动量分别为pA=6.0kg•m/s,pB=8.0kg•m/s.A追上B并与B相碰,碰后A、B的动量分别为pA′和pB′,pA′、pB′的值可能为( )
 如图所示,A、B两小物块在光滑水平面上沿同一直线同向运动,动量分别为pA=6.0kg•m/s,pB=8.0kg•m/s.A追上B并与B相碰,碰后A、B的动量分别为pA′和pB′,pA′、pB′的值可能为( )
如图所示,A、B两小物块在光滑水平面上沿同一直线同向运动,动量分别为pA=6.0kg•m/s,pB=8.0kg•m/s.A追上B并与B相碰,碰后A、B的动量分别为pA′和pB′,pA′、pB′的值可能为( )| A. | pA′=pB′=7.0kg•m/s | B. | pA′=3.0kg•m/s,pB′=11.0kg•m/s | ||
| C. | pA′=-2.0kg•m/s,pB′=16.0kg•m/s | D. | pA′=-6.0kg•m/s,pB′=20.0kg•m/s |