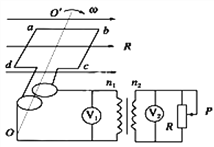
题目内容
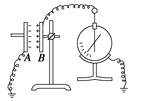
【题目】质量为M=1kg的箱子静止在光滑水平面上,箱子内侧的两壁间距为l=2m,另一质量也为m=1kg且可视为质点的物体从箱子中央以v0=6m/s的速度开始运动,如图所示。已知物体与箱底的动摩擦因数为μ=0.5,物体与箱壁间发生的是完全弹性碰撞,g=l0m/s2。试求:
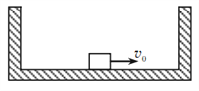
(1)物体可与箱壁发生多少次碰撞?
(2)从物体开始运动到刚好停在箱子上,箱子在水平面上移动的距离是多少?
【答案】(1)物体只与箱子的右侧碰撞一次后便停在箱子上距离右侧0.8m处。
(2)箱子在水平面上移动的距离为x =1.7m
【解析】(1)由于系统要克服摩擦力做功,物体最终会停在箱子上并以相同的速度v向右运动,根据动量守恒有![]()
根据功能关系有![]()
解得物体相对箱子移动的距离s =1.8m
由于箱子内侧的两壁间距为l=2m,故物体只与箱子的右侧碰撞一次后便停在箱子上距离右侧0.8m处。
(2)设碰前物体对地位移为x1,速度为v1;箱子对地位移为x2,速度的为v2(< v1)。则有
![]()
![]()
![]()
![]()
设碰后物体与箱子的速度分别为v1′和v2′,在碰撞过程中有
![]()
![]()
随后木箱向右做匀减速运动,物体向右做匀加速运动,直至速度都变为v。在此过程中,设木箱移动的距离为x2′,则
![]()
故从物体开始运动到刚好停在箱子上,箱子在水平面上移动的距离为
x = x2+ x2′=1.7m

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目