题目内容
如图所示,两木块质量分别为m1和m2,两轻质弹簧的劲度系数分别为kl和k2,上面的木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧,在这过程中,两木块的重力势能各增加多少?

【答案】
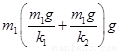
【解析】劲度系数为k1的轻弹簧处于压缩状态,压缩量为: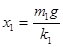
处于拉伸状态时的拉伸量为: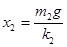
开始平衡时,劲度系数为k2的轻弹簧处于压缩状态,压缩量为: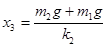
物块2重力势能增加了: =
= 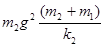
物块1重力势能的增加量为:
思路分析:开始时两弹簧均处于压缩状态,劲度系数为k1的轻弹簧的弹力大小等于质量为m1物块的重力,劲度系数为k2的轻弹簧的弹力大小等于质量为m1、m2的物块总重力.当施力将物块1缓缦地竖直上提,直到下面那个弹簧的下端刚脱离桌面时,下面的弹簧恢复到原长,而上面的弹簧却处于拉伸状态.因此通过胡克定律算出两个弹簧的变化量,从而算出物块2和物块1的重力势能的增加量.
试题点评:劲度系数为k1的轻弹簧本身处于压缩,之后处于拉伸,所以通过胡克定律求出两形变量相加.而劲度系数为k2的轻弹簧本来处于压缩,之后恢复原长,因此求解弹簧问题注意要用动态的思想进行.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
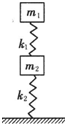 如图所示,两木块质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1,和k2,上面木块压在弹簧上(但不拴接),整个系统处于静止状态.现缓慢向上提m1木块,直到m1木块刚离开上面弹簧,在这过程中下面木块移动的距离为
如图所示,两木块质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1,和k2,上面木块压在弹簧上(但不拴接),整个系统处于静止状态.现缓慢向上提m1木块,直到m1木块刚离开上面弹簧,在这过程中下面木块移动的距离为 A.
A. [来源:Z|xx|k.Com]
[来源:Z|xx|k.Com]