题目内容
 如图所示,一弹性轻绳的一端固定于O点,另一端系一重物A,开始时,物体静止在水平面上,并对水平面有压力,在B处有一与绳垂直的光滑杆,OB为弹性轻绳的自然长度,现有一水平拉力F使物体A沿水平面缓慢移动,(已知弹性绳上产生的弹力与绳的伸长量成正比,且整个过程绳处于弹性限度内)
如图所示,一弹性轻绳的一端固定于O点,另一端系一重物A,开始时,物体静止在水平面上,并对水平面有压力,在B处有一与绳垂直的光滑杆,OB为弹性轻绳的自然长度,现有一水平拉力F使物体A沿水平面缓慢移动,(已知弹性绳上产生的弹力与绳的伸长量成正比,且整个过程绳处于弹性限度内)(1)试分析此过程中物体A受到的摩擦力的变化情况.
(2)已知物体A的质量是m=5kg,物体与地面间的动摩擦因数μ=0.5,当绳与水平面的夹角为37°时,拉力F恰为50N,求此时物体受到绳的弹力T和物体与地面间的摩擦力f.
分析:对物体进行受力分析,因为C做缓慢直线运动,每一个位置都可以看成平衡状态,运用正交分解法求出支持力的大小,以及拉力的大小,从而判断摩擦力的变化.根据受力分析,结合力的平行四边形定则,与三角函数,即可求解.
解答:解:物体A在C处受到重力、支持力、水平拉力、弹性绳的拉力和摩擦力.如图.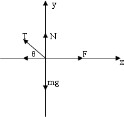
设与B点距地面的高度为h,弹性绳与水平面的夹角为θ,BC长度为x(即形变量),根据正交分解得:
N=mg-kxsinθ=mg-kx?
=mg-kh.
所以支持力不变,摩擦力f=μN,知地面对A的摩擦力保持不变.
(2)当θ=37°时,F=50N,则有:Tsin37°+FN-mg=0
F-Tcos37°-μFN=0
解得:T=
代入数据,解得T=50N;
而f=μFN=μ(mg-Tsin37°)
代入数据,解得f=10N.
答:(1)分析此过程中物体A受到的摩擦力的不变.
(2)此时物体受到绳的弹力T和物体与地面间的摩擦力10N.

设与B点距地面的高度为h,弹性绳与水平面的夹角为θ,BC长度为x(即形变量),根据正交分解得:
N=mg-kxsinθ=mg-kx?
| h |
| x |
所以支持力不变,摩擦力f=μN,知地面对A的摩擦力保持不变.
(2)当θ=37°时,F=50N,则有:Tsin37°+FN-mg=0
F-Tcos37°-μFN=0
解得:T=
| F-μmg |
| (cos37°-μsin37°) |
代入数据,解得T=50N;
而f=μFN=μ(mg-Tsin37°)
代入数据,解得f=10N.
答:(1)分析此过程中物体A受到的摩擦力的不变.
(2)此时物体受到绳的弹力T和物体与地面间的摩擦力10N.
点评:解决本题的关键能够正确地进行受力分析,熟练运用正交分解去求解力.并掌握受力平衡方程,与三角函数知识的运用.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 (2013?黄冈一模)如图所示,一砂袋用无弹性轻细绳悬于O点.开始时砂袋处于静止状态,此后用弹丸以水平速度击中砂袋后均未穿出.第一次弹丸的速度为v0,打入砂袋后二者共同摆动的最大摆角为θ(θ<90°),当其第一次返回图示位置时,第二粒弹丸以另一水平速度v又击中砂袋,使砂袋向右摆动且最大摆角仍为θ.若弹丸质量均为m,砂袋质量为5m,弹丸和砂袋形状大小忽略不计,求两粒弹丸的水平速度之比v0/v为多少?
(2013?黄冈一模)如图所示,一砂袋用无弹性轻细绳悬于O点.开始时砂袋处于静止状态,此后用弹丸以水平速度击中砂袋后均未穿出.第一次弹丸的速度为v0,打入砂袋后二者共同摆动的最大摆角为θ(θ<90°),当其第一次返回图示位置时,第二粒弹丸以另一水平速度v又击中砂袋,使砂袋向右摆动且最大摆角仍为θ.若弹丸质量均为m,砂袋质量为5m,弹丸和砂袋形状大小忽略不计,求两粒弹丸的水平速度之比v0/v为多少?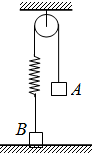 如图所示,一根轻绳跨过一光滑定滑轮,一端连接物块A,另一端通过轻质弹簧连接物块B,设A、B质量分别为mA、mB.B放在地面上,A离地面有足够的高度.当A的质量mA发生改变时,弹簧中弹力的大小也将随之改变.下列四个图象中,能正确反映弹簧弹力与mA之间的关系的是(设弹簧均在弹性限度内) ( )
如图所示,一根轻绳跨过一光滑定滑轮,一端连接物块A,另一端通过轻质弹簧连接物块B,设A、B质量分别为mA、mB.B放在地面上,A离地面有足够的高度.当A的质量mA发生改变时,弹簧中弹力的大小也将随之改变.下列四个图象中,能正确反映弹簧弹力与mA之间的关系的是(设弹簧均在弹性限度内) ( )