题目内容
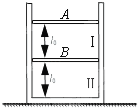
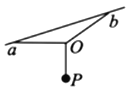
【题目】如图所示,两根轻质细线的一端拴在O点、另一端分别固定在楼道内的倾斜天花板上的a点和b点,一质量为m的重物P通过长度为L的轻质细线固定在O点,系统静止,Oa水平、Ob与竖直方向成一定夹角。现在对重物施加一个水平向右的拉力F,使重物P缓慢移动,至OP间细线转动60°,此过程中拉力F做功W,则下列判断正确的是
A. Oa上的拉力F1可能不变,Ob上的拉力F2可能增大
B. Oa上的拉力F1不断增大,Ob上的拉力F2一定不变
C. ![]()
D. ![]()
【答案】BC
【解析】开始时重物受到重力和绳子的拉力,所以绳子的拉力等于重物的重力;设对重物施加一个水平向右的拉力后细绳与竖直方向之间的拉力为θ,如图,则有:![]()

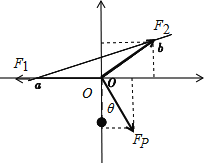
选择节点O点为研究对象,则O点受到三个力的作用处于平衡状态,受力如图;由图可知,在竖直方向:F2沿竖直方向的分力始终等于FPcosθ=mg,而且F2的方向始终不变,所以F2始终不变;沿水平方向:F1的大小等于F2沿水平方向的分力与FP沿水平方向分力的和,由于FP沿水平方向分力随θ的增大而增大,所以F1逐渐增大。故A错误,B正确;根据动能定理可知W=mgL(1-cos60°)=![]() mgL,故C正确、D错误。故选BC。
mgL,故C正确、D错误。故选BC。

练习册系列答案
相关题目