题目内容
【题目】AB两球质量分别为m1与m2用一劲度系数为k的弹相连,一长为L1的细线与m1相连,置于水平光滑桌面上,细线的另一端拴在竖直轴00′上,如图所示。当m1与m2均以角速度ω绕OO′做匀速圆周运动时,弹簧长度为L2,求:
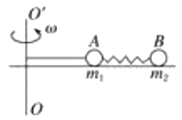
(1)此时弹簧的伸长量;
(2)绳子的弹力;
(3)将线突然烧断瞬间A、B两球的加速度大小分别是多少。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
![]()
【解析】
(1)由题意可知,B球受到的弹簧弹力充当B球做圆周运动的向心力。设弹簧伸长ΔL,满足:![]()
解得弹簧伸长量为:![]()
(2)对A球分析,绳的弹力和弹簧弹力的合力充当A球做匀速圆周运动的向心力。满足:
![]()
所以绳子的弹力为:![]()
(3)绳子烧断的瞬间,A、B两球都由弹簧的弹力提供加速度
A球:![]()
解得:![]()
B球:![]()
解得:![]()

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
【题目】某同学在“用打点计时器测速度”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点.其相邻点间的距离如图所示,每两个相邻的测量点之间的时间间隔为0.10s.

(1)试根据纸带上各个计数点间的距离,每个0.10s测一次速度,计算出打下B、C、D、E、F五个点时小车的瞬时速度,并将各个速度值填入下表(结果要求保留3位有效数字)
vB | vC | vD | vE | vF | |
数值(m/s) | ____ | ____ | ____ | ____ | ____ |
(2)将B、C、D、E、F各个时刻的瞬时速度标在直角坐标系中,并在图中画出小车的瞬时速度随时间变化的关系图线.
(______________)
(3)由v﹣t图象可知打下A点时小车的瞬时速度vA=________,打下G点时小车的瞬时速度vB=________.