题目内容
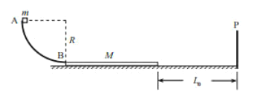
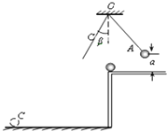
【题目】如图是用来验证动量守恒的实验装置，球1用细线悬挂于O点，O点正下方桌子的边缘放有一静止球2．实验时，将球1拉到A点并从静止开始释放球1，当它摆到悬点正下方时与球2发生对心碰撞．碰撞后，球1把处于竖直方向的轻质指示针OC推移到与竖直线最大夹角为β处，球2落到水平地面上的C点．测出有关数据即可验证1、2两球碰撞时动量守恒．现已测出：在A点时，球1离水平桌面的高度为a，轻质指示针OC与竖直方向的夹角为β，球1和球2的质量分别为m1、m2，C点与桌子边沿间的水平距离为x．
（1）下列有关本实验说法正确的是_______
A．桌面必须水平 B．两球发生的一定是弹性碰撞
C．两球半径必须相等，但质量m1应大于m2
D．为了减小实验误差，应尽量选取半径小密度大的小球
（2）还需要测量的物理量及其符号是_____________和__________________ ；
（3）根据测量的数据，该实验中动量守恒的表达式为 _________________ ．如果还满足______说明两球发生的是弹性碰撞。
【答案】（1） ACD （2）球1 的摆长L 桌面离水平地面的高度h （3）
【解析】
（1）为了保证小球2做平抛运动，所以桌面必须水平，故A对；本题只是研究碰撞过程中动量守恒，所以不要求一定是弹性碰撞，故B错；要保证两球对心碰撞，则必须要求两球半径相等，为了防止碰后球1反弹,故球1的质量应大于球b的质量;故C对；为了保证小球下落过程中是自由落体运动，则应该尽量选取半径小密度大的小球，这样运动中受到的空气阻力会变小，减小误差，故D对；
（2）要通过平抛运动的分位移公式求解碰撞后2球的速度,所以要测量桌面高h；要求出碰后小球A的速度还需要求出球1 的摆长L
（3）小球1从A处下摆过程只有重力做功,机械能守恒,根据机械能守恒定律,有
解得：
碰撞后1小球上升到最高点的过程中,机械能守恒,根据机械能守恒定律,有
解得：
碰撞后小球2做平抛运动,
所以2球碰后速度
,
所以该实验中动量守恒的表达式为
代入数据得：
要证明是弹性碰撞，则必须证明：
整理得：
