Question

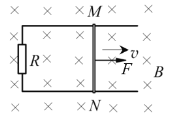
【题目】如图所示，足够长的平行光滑金属导轨固定在水平面上，间距为L，一端连接阻值为R的电阻。导轨所在空间存在竖直向下的匀强磁场，磁感应强度为B 。电阻为r的导体棒MN放在导轨上，其长度恰好等于导轨间距，与导轨接触良好。导轨的电阻可忽略不计。在平行于导轨的恒力F作用下，导体棒沿导轨向右匀速运动，速度大小为v。

(1)求导体棒两端的电压；

(2)通过公式推导验证：在时间内，恒力F所做的功W等于电路获得的电能，也等于电路中产生的焦耳热Q；

(3)从微观角度看，导体棒MN中的自由电荷会同时参与沿导体棒方向和垂直导体棒方向的两个分运动，由此会受到两个相应的洛伦兹力，请你通过计算证明：导体棒中一个自由电荷所受的洛伦兹力做的总功为零。（为了方便，可认为导体棒中的自由电荷为正电荷。）

Answer 1

【答案】(1) (2)见解析 (3) 见解析

【解析】

⑴导体棒沿导轨向右匀速运动产生感应电动势

E = BLv

由闭合电路欧姆定律可得，电路中电流

导体棒两端电压

⑵导体棒匀速运动，受力平衡

在时间内，恒力F做功

电路获得的电能

电路中产生的焦耳热

可见，恒力F所做的功等于电路获得的电能，也等于电路中产生的焦耳热Q。

⑶设自由电荷的电荷量为q，沿导体棒定向移动的速率为。

如图所示，沿导体棒方向的洛伦兹力

在时间内，f1做正功

垂直导体棒方向的洛伦兹力

在时间内，f2做负功

所以，即导体棒中一个自由电荷所受的洛伦兹力做的总功为零。