题目内容
(18分) 如图所示,一竖直面内的轨道由粗糙斜面 AB 和半径为R的光滑圆轨道 BCD组成,AB 与 BCD 相切于 B 点,C 为圆轨道的最低点,圆弧BC所对应的圆心角θ=60°。现有一质量为m的物块(可视为质点)从轨道 ABC 上离地面某一高度h(大小可变)处由静止下滑,已知物块与斜面间的动摩擦因数为 ,重力加速度用g表示,求:
,重力加速度用g表示,求:

(1)当 时,物块滑到C点时对轨道的压力FN;
时,物块滑到C点时对轨道的压力FN;
(2)当h为多少时,物块恰能滑到圆轨道的最高点D;
(3)在满足(2)问的条件下,物块将从D点离开圆轨道,则物块即将与轨道首次相碰时的动能为多大?
 ,重力加速度用g表示,求:
,重力加速度用g表示,求:
(1)当
 时,物块滑到C点时对轨道的压力FN;
时,物块滑到C点时对轨道的压力FN;(2)当h为多少时,物块恰能滑到圆轨道的最高点D;
(3)在满足(2)问的条件下,物块将从D点离开圆轨道,则物块即将与轨道首次相碰时的动能为多大?
(1)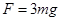 (2)
(2)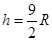 (3)
(3)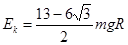
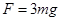 (2)
(2)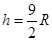 (3)
(3)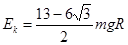
试题分析:(1)过B点作一条水平的辅助线,与图中AG和OC分别交于E和F两点,如图所示
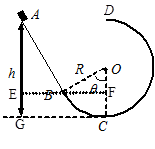
由几何关系易得
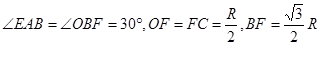
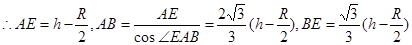
研究从A到C这个过程,根据动能定理
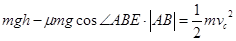
又有
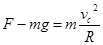 ,所以解得
,所以解得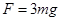
(2)研究从A到D这个过程,根据动能定理
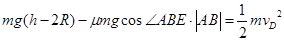 又有
又有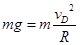 ,所以解得
,所以解得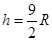
(3)由上问可知
 ,物体脱离D点后作平抛运动,则有
,物体脱离D点后作平抛运动,则有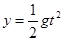 ,假设物体能掉在圆弧上,则令
,假设物体能掉在圆弧上,则令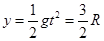 ,此时
,此时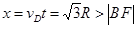 ,假设矛盾,所以物体一定掉在斜面上。
,假设矛盾,所以物体一定掉在斜面上。由几何关系易得D点到斜面上等高点的距离为
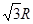
所以由
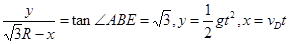 ,解得
,解得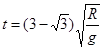
再由
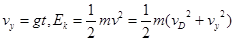 ,解得
,解得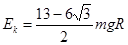

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目

 ,且速度达到最大值vm.设这一过程中电动机的功率恒为P,小车所受阻力恒为F,那么这段时间内
,且速度达到最大值vm.设这一过程中电动机的功率恒为P,小车所受阻力恒为F,那么这段时间内
 mv
mv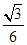 ,轻弹簧下端固定在斜面底端,弹簧处于原长时上端位于B点,开始时物体A到B的距离为L=1 m,现给A一个沿斜面向下的初速度v0=2 m/s,使物体A开始沿斜面向下运动,物体A将弹簧压缩到最短后又恰好被弹回到B点,取g=10 m/s2(不计空气阻力),求:
,轻弹簧下端固定在斜面底端,弹簧处于原长时上端位于B点,开始时物体A到B的距离为L=1 m,现给A一个沿斜面向下的初速度v0=2 m/s,使物体A开始沿斜面向下运动,物体A将弹簧压缩到最短后又恰好被弹回到B点,取g=10 m/s2(不计空气阻力),求: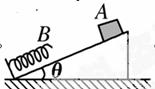


 ="0." 60m的轻细绳,它的一端系住一质量为m的小球P,另一端固定在板上的O点.当平板的倾角固定为
="0." 60m的轻细绳,它的一端系住一质量为m的小球P,另一端固定在板上的O点.当平板的倾角固定为 时,先将轻绳平行于水平轴MN拉直,然后给小球一沿着平板并与轻绳垂直的初速度v0="3." Om/s.若小球能保持在板面内作圆周运动,倾角
时,先将轻绳平行于水平轴MN拉直,然后给小球一沿着平板并与轻绳垂直的初速度v0="3." Om/s.若小球能保持在板面内作圆周运动,倾角 )
)