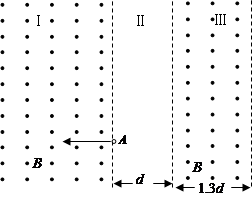题目内容
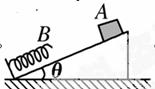
如图所示，倾角为θ＝30°的斜面固定在地面上，物体A与斜面间的动摩擦因数为μ＝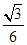
，轻弹簧下端固定在斜面底端，弹簧处于原长时上端位于B点，开始时物体A到B的距离为L＝1 m，现给A一个沿斜面向下的初速度v0＝2 m/s，使物体A开始沿斜面向下运动，物体A将弹簧压缩到最短后又恰好被弹回到B点，取g＝10 m/s2（不计空气阻力），求：
（1）物体A第一次运动到B点时的速度大小；
（2）弹簧的最大压缩量。
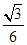，轻弹簧下端固定在斜面底端，弹簧处于原长时上端位于B点，开始时物体A到B的距离为L＝1 m，现给A一个沿斜面向下的初速度v0＝2 m/s，使物体A开始沿斜面向下运动，物体A将弹簧压缩到最短后又恰好被弹回到B点，取g＝10 m/s2（不计空气阻力），求：（1）物体A第一次运动到B点时的速度大小；
（2）弹簧的最大压缩量。
（1）3m/s；（2）0.9m
试题分析：（1）物体A由开始运动直至B点的过程，由动能定理得 mgLsinθ-μmgLcosθ=
-
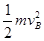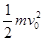
解得
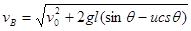，代入数值解得：vB=3m/s（2）设弹簧最大压缩量为x．在物体A刚好接触弹簧直至恰好返回到B点的过程中，由动能定理得
-2μmg x cosθ=0-
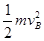，解得：x=0.9m
练习册系列答案
特高级教师点拨系列答案
相关题目
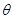=37o的斜直粗糙轨道，bc为一段半径为R=5m的光滑圆弧，圆弧与ab相切于磊点，圆弧圆心O在c点的正上方。已知ab之间高度差H1=5rn，cd之间高度差H2=2．25m，运动员连同滑板的总质量m=60kg。运动员从a点由静止开始下滑后从C点水平飞出，落在轨道上的e点，经短暂的缓冲动作后沿斜面方向下滑。de之间的高度差H3="9" m，运动员连同滑板可视为质点，忽略空气阻力，取g =10m/s2，sin37o=0．6，cos37o=0．8 。求：
，重力加速度用g表示，求：
时，物块滑到C点时对轨道的压力FN；
和
分别是水平向里的匀强磁场的边界，磁场的磁感应强度为B，正方形线框abcd边长为L(L<d)、质量为m，电阻为R。将线框在磁场上方高h处由静止释放，ab边刚进入磁场和穿出磁场时的速度都为
。在线框全部穿过磁场的过程中 
