题目内容
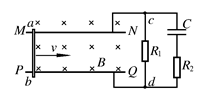
如图所示,两足够长的直平行水平导轨相距 =1.0
=1.0 ,导轨左边连接阻值
,导轨左边连接阻值 =15
=15 的电阻,导轨上放置着
的电阻,导轨上放置着 、
、 两金属捧,
两金属捧, 棒质量
棒质量 =0.75kg、电阻
=0.75kg、电阻 =10
=10 ,
, 棒质量
棒质量 =0.25
=0.25 、电阻
、电阻 =10
=10 ,两金属棒与导轨垂直,两棒靠得很近,之间用长为
,两金属棒与导轨垂直,两棒靠得很近,之间用长为 =4.0m的绝缘轻绳相连,整个装置置于磁感应强度大小B=1.0T、方向竖直向下的匀强磁场中。从
=4.0m的绝缘轻绳相连,整个装置置于磁感应强度大小B=1.0T、方向竖直向下的匀强磁场中。从 =0开始对
=0开始对 棒施加水平向右的拉力
棒施加水平向右的拉力 ,使
,使 棒由静止开始以
棒由静止开始以 =2.0
=2.0 /s2的加速度做匀加速运动,
/s2的加速度做匀加速运动, =2.0s时撤去拉力
=2.0s时撤去拉力 。已知
。已知 棒右边的导轨是光滑的,轻绳绷紧前
棒右边的导轨是光滑的,轻绳绷紧前 棒静止不动,轻绳绷紧后,两棒以相同速度运动直至停止。导轨电阻不计。求:
棒静止不动,轻绳绷紧后,两棒以相同速度运动直至停止。导轨电阻不计。求:
(1)拉力 随时间
随时间 变化的关系式;
变化的关系式;
(2)轻绳绷紧后,电阻R上产生的焦耳热;
 =1.0
=1.0 ,导轨左边连接阻值
,导轨左边连接阻值 =15
=15 的电阻,导轨上放置着
的电阻,导轨上放置着 、
、 两金属捧,
两金属捧, 棒质量
棒质量 =0.75kg、电阻
=0.75kg、电阻 =10
=10 ,
, 棒质量
棒质量 =0.25
=0.25 、电阻
、电阻 =10
=10 ,两金属棒与导轨垂直,两棒靠得很近,之间用长为
,两金属棒与导轨垂直,两棒靠得很近,之间用长为 =4.0m的绝缘轻绳相连,整个装置置于磁感应强度大小B=1.0T、方向竖直向下的匀强磁场中。从
=4.0m的绝缘轻绳相连,整个装置置于磁感应强度大小B=1.0T、方向竖直向下的匀强磁场中。从 =0开始对
=0开始对 棒施加水平向右的拉力
棒施加水平向右的拉力 ,使
,使 棒由静止开始以
棒由静止开始以 =2.0
=2.0 /s2的加速度做匀加速运动,
/s2的加速度做匀加速运动, =2.0s时撤去拉力
=2.0s时撤去拉力 。已知
。已知 棒右边的导轨是光滑的,轻绳绷紧前
棒右边的导轨是光滑的,轻绳绷紧前 棒静止不动,轻绳绷紧后,两棒以相同速度运动直至停止。导轨电阻不计。求:
棒静止不动,轻绳绷紧后,两棒以相同速度运动直至停止。导轨电阻不计。求:(1)拉力
 随时间
随时间 变化的关系式;
变化的关系式;(2)轻绳绷紧后,电阻R上产生的焦耳热;

(1) ,
, ≤2.0
≤2.0 (2)0.375J
(2)0.375J
 ,
, ≤2.0
≤2.0 (2)0.375J
(2)0.375J(1)B棒运动时,其速度为:
感应电动势为:
电路总电阻为:
感应电流:
金属棒 受安培力为:
受安培力为:
对金属棒,由牛顿定律得: ma
ma
从而解得 随
随 变化的关系式为:
变化的关系式为: ,
, ≤2.0
≤2.0 (8分)
(8分)
(2)2.0s内B棒发生的位移为: ,即撤去拉力
,即撤去拉力 时绳恰好绷紧,
时绳恰好绷紧,
2.0s时,B棒的速度为:
绳绷紧时满足动量守恒:
绳绷紧后,AB共同切割磁感线,其内阻
所以,电阻R上产生的热等为: (10分)
(10分)

感应电动势为:

电路总电阻为:

感应电流:

金属棒
 受安培力为:
受安培力为:
对金属棒,由牛顿定律得:
 ma
ma从而解得
 随
随 变化的关系式为:
变化的关系式为: ,
, ≤2.0
≤2.0 (8分)
(8分)(2)2.0s内B棒发生的位移为:
 ,即撤去拉力
,即撤去拉力 时绳恰好绷紧,
时绳恰好绷紧,2.0s时,B棒的速度为:

绳绷紧时满足动量守恒:

绳绷紧后,AB共同切割磁感线,其内阻

所以,电阻R上产生的热等为:
 (10分)
(10分)
练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目




 如图所示,磁感应强度大小B=0.15T,方向垂直纸面向里的匀强磁场分布在半径为R=0.10m的圆形区域内,圆的左端跟
如图所示,磁感应强度大小B=0.15T,方向垂直纸面向里的匀强磁场分布在半径为R=0.10m的圆形区域内,圆的左端跟 轴相切于直角出标系的原点
轴相切于直角出标系的原点 ,右端边界MN相切于
,右端边界MN相切于 轴的A点。MN右侧有方向平行于
轴的A点。MN右侧有方向平行于 的带正电的粒子流,荷质比
的带正电的粒子流,荷质比 ,粒子重力不计。右侧场强大小
,粒子重力不计。右侧场强大小 。现以过
。现以过 ;
; ;
; 为多大?
为多大?

 ="L,"
="L,"  =2L,整个线框处于竖直方向的匀强磁场中,磁场的磁感应强度为B,导线框上各段导线的电阻与其长度成正比,已知该种电阻丝单位长度上的电阻为
=2L,整个线框处于竖直方向的匀强磁场中,磁场的磁感应强度为B,导线框上各段导线的电阻与其长度成正比,已知该种电阻丝单位长度上的电阻为 ,
,
 在垂直于框面的水平磁场中,运动一段时间后速度恒定为v,运动过程中总有两条边处在竖直方向,即线框不转动,如图所示。已知磁场的磁感应强度在竖直方 向按
在垂直于框面的水平磁场中,运动一段时间后速度恒定为v,运动过程中总有两条边处在竖直方向,即线框不转动,如图所示。已知磁场的磁感应强度在竖直方 向按 规律逐渐增大,k为常数。试求水平初速度
规律逐渐增大,k为常数。试求水平初速度