题目内容
【题目】在直角坐标系xoy中,x轴上方空间分布着竖直向上的匀强电场,场强大小为![]() 。在第一象限(包括x和y轴的正方向)存在垂直坐标平面的周期性变化的磁场,磁感应强度的大小
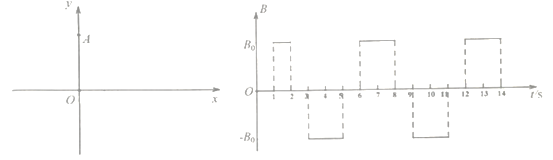
。在第一象限(包括x和y轴的正方向)存在垂直坐标平面的周期性变化的磁场,磁感应强度的大小![]() ,变化规律如图所示,规定垂直坐标平面向外为磁场正方向。一带量为+q、质量为m的小球P被锁定在坐标原点,带电小球可视为质点。t=0时刻解除对P球的锁定,1s末带电小球P运动到y轴上的A点。此后匀强电场方向不变,大小变为原来的一半。已知重力加速度为10m/s2,求:
,变化规律如图所示,规定垂直坐标平面向外为磁场正方向。一带量为+q、质量为m的小球P被锁定在坐标原点,带电小球可视为质点。t=0时刻解除对P球的锁定,1s末带电小球P运动到y轴上的A点。此后匀强电场方向不变,大小变为原来的一半。已知重力加速度为10m/s2,求:
(1)小球P运动到A点时的速度大小和位移大小;
(2)定性画出小球P运动的轨迹(至少在磁场中两个周期)并求出小球进入磁场后的运动周期;
(3)若周期性变化的磁场仅存在于某矩形区域内,区域左边界与y轴重合,下边界与过A点平行于x轴的直线重合。为保证带电小球离开磁场时的速度方向沿y轴正方向,则矩形磁场区域的水平及竖直边长应同时满足什么条件?
【答案】(1)![]() ,
,![]() ;(2)
;(2)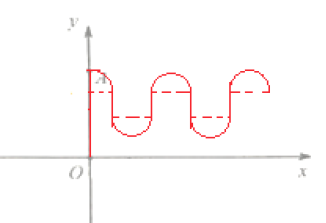 ,6s;(3)
,6s;(3)![]() ,
,![]()
【解析】
(1)根据牛顿第二定律和运动学公式得
![]()
![]()
![]()
代入数据解得![]() ,
,![]()
(2)根据题意,画出其运动轨迹,如图所示

1s末小球进入磁场后,由于小球所受重力和电场力平衡,小球在洛伦兹力作用下做匀速圆周运动,根据牛顿第二定律可得
![]()
圆周运动周期
![]()
由B-t图象可知,小球在1-2s顺时针旋转四分之一圆周,接下来2-3s做匀速直线运动,3-5s逆时针旋转半个圆周,5-6s做匀速直线运动,6-7s顺时针旋转四分之一圆周,完成一次周期性运动。即带电小球在复合场中运动的周期T=6s
(3)带电小球1s内做匀速直线运动的位移
![]()
要使带电小球沿y轴正方向离开磁场需满足
![]()
![]()
根据洛伦兹力提供向心力,则有
![]()
解得
![]() ,
,![]()

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目