题目内容
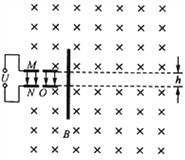
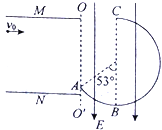
【题目】一质量为m1=1 kg,带电荷量为q=+0. 5 C的小球以速度v0=3 m/s,沿两正对带电平行金属板(板间电场可看成匀强电场)左侧某位置水平向右飞入,极板长0. 6 m,两极板间距为0.5 m,不计空气阻力,小球飞离极板后恰好由A点沿切线落入竖直光滑圆弧轨道ABC,圆弧轨道ABC的形状为半径R<3m的圆截去了左上角127°的圆弧,CB为其竖直直径,在过A点竖直线OO′的右边界空间存在竖直向下的匀强电场,电场强度为E=10 V/m.(g=10m/s2)求:
(1)两极板间的电势差大小U;
(2)欲使小球在圆弧轨道运动时不脱离圆弧轨道,求半径R的取值应满足的条件.
(3)若在B处放一个质量为m2光滑绝缘小球,且m2=m1,两球相碰为弹性正碰,若m2球能运动到圆弧轨道最高点,求圆弧轨道半径的范围.
【答案】(1)10 V (2)![]() ;
;![]() 或
或![]() (3)
(3)![]()
【解析】⑴在 A 点vy= v0tan 53°= 4 m/s
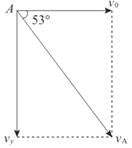
带电粒子在平行板中t=L/v0 = 0.2 s
vy = at, a= 20 m/s2
又 mg+Eq=ma E=U/d 得U=10 V
(2)在A点速度vA = 5 m/s
i.若小球不超过圆心等高处![]()
![]()
ii.若小球能到达最高点C
![]()
在 C 点:![]() 可得
可得![]()
可知:![]()
故圆弧軌道半径R的取值条件为:
![]() 或
或 ![]()
(3)m1球运动B处
![]()
m1球与m2球是弹性碰撞且质量相等,根据动量和能量守恒知两者碰后交換速度 v1=0,v2=vB
对m2球能运动到C点应满足条件:![]()
![]()
解得:![]()
可得;![]()

练习册系列答案
相关题目