题目内容
【题目】如图所示为一种粒子加速器的原理图.图中M、N为带有小孔的水平平行板,板上接有恒定电压U,板间距离为h,以M、N板所在平面为界,上方和下方有垂直于纸面向里的范围足够大的匀强磁场,磁感应强度大小相等.质量为m、电荷量为q的带正电粒子在M板小孔处由静止释放,在板间电压的加速下从N板小孔O射入磁场。为了测量磁场磁感应强度的大小,在板的右侧放置一竖直的荧光屏,当荧光屏在靠近板的右端位置时,粒子能打到荧光屏上,向右缓慢移动荧光屏,且不断释放粒子,结果发现荧光屏离O点距离为d时,粒子打在荧光屏上的位置第一次达到最低.荧光屏足够大,不计粒子的重力,不考虑相对论效应、两金属板间电场的边际效应以及电场变化对于外部磁场和粒子运动的影响.求:
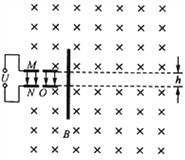
(1)磁场的磁感应强度大小;
(2)将荧光屏拿走,粒子将多次运动到N板所在的平面,求粒子运动轨迹与N板所在平面的交点到O点的距离;
(3)若粒子经过4次加速后回到M板小孔处,求粒子运动的总时间.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】(1)粒子经加速电场加速![]()
得:![]()
由题意可知,粒子在磁场中做圆周运动的半径r1=d
由![]()
求得:![]()
(2)粒子经过n次加速,则![]()
解得:![]()
![]()
求得![]()
(3)粒子经过4次加速后回到M板小孔处,则在磁场中运动的时间
![]()
设在电场中运动的时间为t2,则![]()
![]()
求得![]()
设粒子在无场区域运动的时间为t3,则![]()
求得![]()
因此运动的总时间![]()

练习册系列答案
相关题目