题目内容
.如图13-11所示，ABCD是折射率n=1.5，截面为矩形的均匀玻璃砖，一束平行光从空气入射到AB面上然后折射向BC面时，那么：（1）若AB面长度为L，要使所有入射光都能折射到BC面时，BC面最少应是多少？（2）这些折射光线能否从BC面射出？如果不能从BC面射出，需改变什么条件才能使折射光线从BC面射出？
图13-11
图13-11
要使入射光线能折射到BC面首要的是平行光束是斜入射，在这个前提下，只需讨论最边缘的PA这条光线能射到BC面的条件.要使BC长度最短，就要使平行光束的入射角增大.其极值是90°，此即为入射角，光应折向光密介质，折射角正好是临界角C，sinC=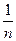
，
即BC=ABctgC=L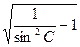
=L
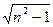
根据上述分析可行，经AB面折射后，最大折射角r1＜C,即r1＜40°40′.这样在BC面的入射角最小是i2=90°-41°49′=48°11′，BC即最小的入射角，仍大于从玻璃砖射入空气发生全反射的临界角，因此，在BC面只发生全反射,光线不可能折射出去.
要想从BC面射出,改变玻璃砖的几何条件是不行的，只能改变其光学特性，即改变其折射率.由于折射角r1是小于临界角C，因此光线要能射出，必须同时使在BC面的入射角r2也小于临界角C，即r1＞C，且90°-r1＜C，即C＜45°，由sinC=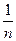可得n＜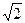
.
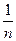，即BC=ABctgC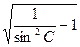=L
=L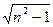根据上述分析可行，经AB面折射后，最大折射角r1＜C,即r1＜40°40′.这样在BC面的入射角最小是i2=90°-41°49′=48°11′，BC即最小的入射角，仍大于从玻璃砖射入空气发生全反射的临界角，因此，在BC面只发生全反射,光线不可能折射出去.
要想从BC面射出,改变玻璃砖的几何条件是不行的，只能改变其光学特性，即改变其折射率.由于折射角r1是小于临界角C，因此光线要能射出，必须同时使在BC面的入射角r2也小于临界角C，即r1＞C，且90°-r1＜C，即C＜45°，由sinC=
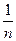可得n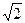＜.作出光路图，由几何关系和全反射的条件综合进行分析求解.
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
，然后确定圆心的位置，记在玻璃砖上
.两条平行光线垂直于棱镜底面入射，如图13-3所示.两条光线由棱镜射出时所成的角度为（ ）
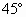，光束中包含两种波长的光，玻璃对这两种波长的光的折射率分别为
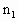＝1.5，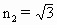
，请回答以下问题：
