Question

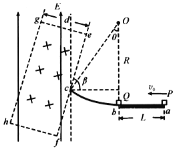
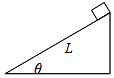
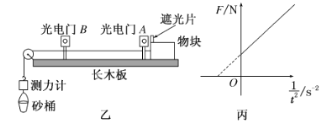
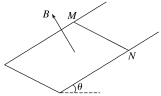
【题目】如图所示，足够长的U形导体框架的宽度L＝0.5 m，电阻可忽略不计，其所在平面与水平面成θ＝37°。有一磁感应强度B＝0.8 T的匀强磁场，方向垂直于导体框平面。一根质量m＝0.4 kg、电阻R＝1 Ω的导体棒MN垂直跨放在U形框架上，某时刻起将导体棒由静止释放。已知导体棒与框架间的动摩擦因数μ＝0.5.(sin 37°＝0.6，cos 37°＝0.8，g取10 m/s2)

求:

(1)导体棒刚开始下滑时的加速度大小；

(2)导体棒运动过程中的最大速度；

(3)从导体棒开始下滑到速度刚达到最大时的过程中，通过导体棒横截面的电荷量Q＝4 C，求导体棒在此过程中消耗的电能。

Answer 1

【答案】(1)2m/s2；(5)5m/s；(3)3J

【解析】

(1)导体棒刚开始下滑时，其受力情况如图甲，根据牛顿第二定律有:

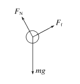
mgsinθ－μmgcosθ＝ma①

解得a＝2m/s2②

(2)当导体棒匀速下滑时具有最大速度v，其受力情况如图乙，则在平行斜面方向上有:

mgsinθ－μmgcosθ－F＝0③

安培力：F＝BIL④

回路中电流：⑤

MN棒中产生的电动势E=BLv⑥

由以上各式得：⑦

代入数值得v=5m/s⑧

(3)通过导体棒横截面的电荷量: ⑨

⑩

设导体棒下滑速度刚好为v时的位移为x，则ΔΦ＝BxL⑾

全程对棒由动能定理：(12)

其中W安为克服安培力做的功。

由功能关系，克服安培力做的功等于导体棒在此过程中消耗的电能，即

QR=W=3J(13)