题目内容
 (2011?福州模拟)如图在xoy坐标系第Ⅰ象限,磁场方向垂直xoy平面向里,磁感应强度大小均为B=1.0T;电场方向水平向右,电场强度大小均为E=
(2011?福州模拟)如图在xoy坐标系第Ⅰ象限,磁场方向垂直xoy平面向里,磁感应强度大小均为B=1.0T;电场方向水平向右,电场强度大小均为E=| 3 |
(1)带电粒子在xoy平面内做匀速直线运动的速度v0大小和方向;
(2)带电粒子在xoy平面内做匀速圆周运动时电场强度的大小和方向;
(3)若匀速圆周运动时恰好未离开第Ⅰ象限,x轴上入射P点应满足何条件?
分析:(1)粒子在复合场中做匀速直线运动,受力平衡,受力分析后应用平衡条件求解即可.
(2)带电粒子在xoy平面内做匀速圆周运动时,电场力F电必须与重力平衡,洛伦兹力提供向心力.
(3)带电粒子匀速圆周运动恰好未离开第1象限,圆弧左边与y轴相切,画出图象,找出轨道半径,利用洛伦兹力提供向心力公式计算即可.
(2)带电粒子在xoy平面内做匀速圆周运动时,电场力F电必须与重力平衡,洛伦兹力提供向心力.
(3)带电粒子匀速圆周运动恰好未离开第1象限,圆弧左边与y轴相切,画出图象,找出轨道半径,利用洛伦兹力提供向心力公式计算即可.
解答: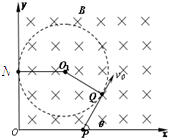 解:(1)如图粒子在复合场中做匀速直线运动,设速度v0与x轴夹角为θ,依题意得:
解:(1)如图粒子在复合场中做匀速直线运动,设速度v0与x轴夹角为θ,依题意得:
重力mg=2.0×10-6N,电场力F电=Eq=2
×10-6N
洛伦兹力:f洛=
=4.0×10-6N
由f洛=qvB得 v0=2 m/s
tanθ=
所以:θ=60°
速度v0大小2m/s,方向斜向上与x轴夹角为60°
(2)带电粒子在xOy平面内做匀速圆周运动时,电场力F电必须与重力平衡,洛伦兹力提供向心力.故电场强度:E=
=1N/C,方向竖直向上.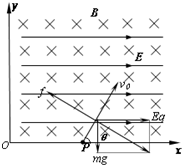
(3)如图带电粒子匀速圆周运动恰好未离开第1象限,圆弧左边与y轴相切N点;
PQ匀速直线运动,PQ=v0t=0.2 m
洛伦兹力提供向心力:qv0B=m
,整理并代入数据得R=0.2m
由几何知识得:OP=R+Rsin60°=PQcos60°=0.27m
故:x轴上入射P点离O点距离至少为0.27m
答:(1)带电粒子在xoy平面内做匀速直线运动的速度v0大小2m/s,方向斜向上与x轴夹角为60°
(2)带电粒子在xoy平面内做匀速圆周运动时电场强度的大小1N/C,方向竖直向上.
(3)若匀速圆周运动时恰好未离开第Ⅰ象限,x轴上入射P点距离至少为0.27m
 解:(1)如图粒子在复合场中做匀速直线运动,设速度v0与x轴夹角为θ,依题意得:
解:(1)如图粒子在复合场中做匀速直线运动,设速度v0与x轴夹角为θ,依题意得:重力mg=2.0×10-6N,电场力F电=Eq=2
| 3 |
洛伦兹力:f洛=
| (qE)2+(mg)2 |
由f洛=qvB得 v0=2 m/s
tanθ=
| qE |
| mg |
| 3 |
所以:θ=60°
速度v0大小2m/s,方向斜向上与x轴夹角为60°
(2)带电粒子在xOy平面内做匀速圆周运动时,电场力F电必须与重力平衡,洛伦兹力提供向心力.故电场强度:E=
| mg |
| q |

(3)如图带电粒子匀速圆周运动恰好未离开第1象限,圆弧左边与y轴相切N点;
PQ匀速直线运动,PQ=v0t=0.2 m
洛伦兹力提供向心力:qv0B=m
| ||
| R |
由几何知识得:OP=R+Rsin60°=PQcos60°=0.27m
故:x轴上入射P点离O点距离至少为0.27m
答:(1)带电粒子在xoy平面内做匀速直线运动的速度v0大小2m/s,方向斜向上与x轴夹角为60°
(2)带电粒子在xoy平面内做匀速圆周运动时电场强度的大小1N/C,方向竖直向上.
(3)若匀速圆周运动时恰好未离开第Ⅰ象限,x轴上入射P点距离至少为0.27m
点评:带电粒子在电磁场中的运动一般有匀速直线运动、圆周运动和一般的曲线运动;匀速直线运动一般平衡条件求解,圆周运动由洛仑兹力充当向心力,一般的曲线运动一般由动能定理求解.临界问题需要画出运动轨迹,找出临界条件进行求解.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目

