题目内容
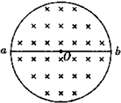
如图所示,在真空中半径r=3.0×10
-2m的圆形区域内,有磁感应强度B=0.2T,方向如图的匀强磁场,一束带正电的粒子以初速度v
0=1.0×10
6m/s,从磁场边界上直径ab的a端沿各个方向射入磁场,且初速方向都垂直于磁场方向,若该束粒子的比荷
=1.0×108C/kg,不计粒子重力.求:
(1)粒子在磁场中运动的最长时间.
(2)若射入磁场的速度改为v=3.0×10
5m/s,其他条件不变,求磁场边界上有粒子击中的弧长.(sin37°=0.6,cos37°=0.8)
分析:①首先做出轨迹图,利用几何关系判断出当弦长为多少时运动时间最长,从而可以计算出粒子在磁场中运行的最长时间.
②由确定的速度先求出粒子在磁场中的运动半径,利用几何关系判断出粒子射出磁场的区域,从而计算粒子射出区域弧长.
解答: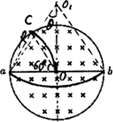
解:
①、由洛伦兹力提供向心力得:
=Bqv0解得:
R==0.05m>r故以ab为弦长的圆弧对应运动时间最长.
由图可知:
sinθ==∴θ=37°
∴
t=×=6.45×10-8s②、若速率v=3.0×10
5m/s.则
R′==0.015m,
由图可知有粒子可击中的边界弧长为
,由几何关系可知弧长为
所对应的圆心角为60°
=
×2πr=3.14×10-2m
答:(1)粒子在磁场中运动的最长时间为6.45×10
-8s.
(2)磁场边界上有粒子击中的弧长为3.14×10
-2m.
点评:解决带电粒子在匀强磁场中匀速圆周运动问题时,应首先确定圆心的位置,找出半径,做好草图,利用数学几何并结合运动规律进行求解.
(1)圆心的确定:因洛伦兹力始终指向圆心,根据洛伦兹力的方向与速度的方向垂直,画出粒子运动轨迹中的任意两点(一般是射入和射出磁场的两点)的洛伦兹力的方向,其延长线的交点即为圆心.
(2)半径的确定和计算,半径的计算一般是利用几何知识,常用解三角形的方法.
(3)在磁场中运动时间的确定,由求出t,t=
T(θ为弧度)或t=
T(θ为度数);应注意速度矢量转过的角度θ,就是圆半径转过的角度,以及弦切角与圆心角的关系.
 一题一题找答案解析太慢了
一题一题找答案解析太慢了
下载作业精灵直接查看整书答案解析立即下载
练习册系列答案
相关题目
 如图所示,在真空中半径r=3.0×10-2m的圆形区域内,有磁感应强度B=0.2T,方向如图的匀强磁场,一束带正电的粒子以初速度v0=1.0×106m/s,从磁场边界上直径ab的a端沿各个方向射入磁场,且初速方向都垂直于磁场方向,若该束粒子的比荷
如图所示,在真空中半径r=3.0×10-2m的圆形区域内,有磁感应强度B=0.2T,方向如图的匀强磁场,一束带正电的粒子以初速度v0=1.0×106m/s,从磁场边界上直径ab的a端沿各个方向射入磁场,且初速方向都垂直于磁场方向,若该束粒子的比荷 解:
解: 解:
解:




 半圆柱形玻璃砖的圆心在O点,一束红光和一束紫光从不同角度对准O点射向玻璃砖,如图所示.结果两种色光都沿OC方向射出,则( )
半圆柱形玻璃砖的圆心在O点,一束红光和一束紫光从不同角度对准O点射向玻璃砖,如图所示.结果两种色光都沿OC方向射出,则( )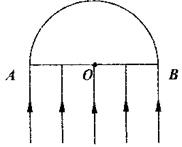 单色平行光a垂直射向一半径为R的玻璃半球的平面,其截面如图所示,发现半圆弧ACB上只有
单色平行光a垂直射向一半径为R的玻璃半球的平面,其截面如图所示,发现半圆弧ACB上只有

 区域有光射出(不考虑光反射后)的折射光线.若将单色平行光a换成单色平行光b,发现半圆弧ACB上只有
区域有光射出(不考虑光反射后)的折射光线.若将单色平行光a换成单色平行光b,发现半圆弧ACB上只有 区域有光射出(同样不考虑光反射后的折射光线).则下列说法正确的是( )
区域有光射出(同样不考虑光反射后的折射光线).则下列说法正确的是( )