题目内容
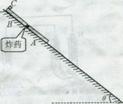
如图所示,在倾角为![]() 的足够长的光滑斜面上,质量均为M=2 kg的木板
的足够长的光滑斜面上,质量均为M=2 kg的木板![]() 和
和![]() 之间夹有少许炸药,在
之间夹有少许炸药,在![]() 的上端放有一质量为
的上端放有一质量为![]() kg的物体
kg的物体![]() (可视为质点),
(可视为质点),![]() 与
与![]() 之间的动摩擦因数
之间的动摩擦因数![]() =0.75。现由静止同时释放它们,当它们沿斜面滑行距离
=0.75。现由静止同时释放它们,当它们沿斜面滑行距离![]() =3 m时炸药瞬间爆炸,爆炸完毕时
=3 m时炸药瞬间爆炸,爆炸完毕时![]() 的速度
的速度![]() =12 m/s,此后,
=12 m/s,此后,![]() 始终未从
始终未从![]() 的上表面滑落,求木板
的上表面滑落,求木板![]() 至少多长?(假设爆炸不会影响各物体的质量、形状和各表面的光滑程度。取
至少多长?(假设爆炸不会影响各物体的质量、形状和各表面的光滑程度。取![]()
![]()
![]() )
)
解:
整体下滑阶段,研究A、B、C整体,由动能定理,设末速为v,有:
![]() (2分)
(2分)
得:v=6m/s (1分)
爆炸前后,研究A和B,由动量守恒定律有:
![]() (2分)
(2分)
得:vB=0 (1分)
此后,C在B上滑动的加速度aC,由牛顿第二定律得:
![]() (2分)
(2分)
得:aC=0 (1分)
对B有:
![]() (2分)
(2分)
得:aB=9m/s2 (1分)
A和B达到共同速度v后将不再相对滑动,设这段时间为t,有:
![]() (2分)
(2分)
![]() (1分)
(1分)
板的最小长度L满足:
![]() (2分)
(2分)
解得:L=2m (1分)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,在倾角为θ的光滑斜面上,一根细绳通过定滑轮分别与木板、小滑块(可视为质点)相连,小滑块质量为m,木板质量为M,木板长为L,小滑块与木板间的动摩擦因数为μ,开始时小滑块静止在木板的上端,现用与斜面平行的拉力F将小滑块缓慢拉至木板的下端,则在此过程中( )
如图所示,在倾角为θ的光滑斜面上,一根细绳通过定滑轮分别与木板、小滑块(可视为质点)相连,小滑块质量为m,木板质量为M,木板长为L,小滑块与木板间的动摩擦因数为μ,开始时小滑块静止在木板的上端,现用与斜面平行的拉力F将小滑块缓慢拉至木板的下端,则在此过程中( ) 如图所示,在倾角为θ的光滑斜面上,放置一根长为L、质量为M、通有电流I的导体棒.重力加速度为g.
如图所示,在倾角为θ的光滑斜面上,放置一根长为L、质量为M、通有电流I的导体棒.重力加速度为g. 如图所示,在倾角为θ的光滑斜面上有一光滑档板A,在档板和斜面之间夹一质量为m的重球B,开始板A处于竖直位置,现使其下端绕O沿逆时针方向缓慢转至水平位置,分析重球B对斜面和对档板压力的变化情况是( )
如图所示,在倾角为θ的光滑斜面上有一光滑档板A,在档板和斜面之间夹一质量为m的重球B,开始板A处于竖直位置,现使其下端绕O沿逆时针方向缓慢转至水平位置,分析重球B对斜面和对档板压力的变化情况是( ) (2011?静安区一模)如图所示,在倾角为α的斜面的顶点将小球水平抛出,若抛出时的初速度较大,小球落到斜面上时的速度也较大,因此有人猜想“小球落到斜面上的速度与平抛的初速度成正比”.这个猜想是
(2011?静安区一模)如图所示,在倾角为α的斜面的顶点将小球水平抛出,若抛出时的初速度较大,小球落到斜面上时的速度也较大,因此有人猜想“小球落到斜面上的速度与平抛的初速度成正比”.这个猜想是 如图所示,在倾角为θ的绝缘斜面上,有相距为L的A、B两点,分别固定着两个带电量均为Q的正点电荷.O为AB连线的中点,a、b是AB连线上两点,其中Aa=Bb=
如图所示,在倾角为θ的绝缘斜面上,有相距为L的A、B两点,分别固定着两个带电量均为Q的正点电荷.O为AB连线的中点,a、b是AB连线上两点,其中Aa=Bb=