题目内容
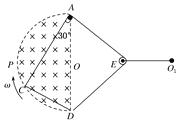
【题目】如图所示,光滑杆弯曲成相互垂直的两段后固定于竖直平面内,A和C两点在同一水平线上,AB=4m,BC=3m.一个质量m的小环套在杆上,以初速度v0=10m/s从A点沿杆上滑.不计小环经过B点时的能量损失,g取10m/s2.则:
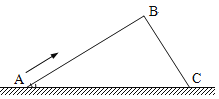
(1)小环在AB段运动的加速度为多少?
(2)小环运动到B点时的速度为多少?
(3)若杆不光滑,各部分粗糙程度均相同.要使小环能够到达C点,小环和杆之间的动摩擦因数μ应小于多少?
【答案】(1)6m/s2方向沿AB杆向下(2)7.2m/s(3)0.8125
【解析】(1)小环在AB段运动过程中,根据牛顿第二定律:mgsinα=ma
代入数据得:a=6m/s2
加速度方向沿AB杆向下
(2)根据运动学公式,有vB2-v02=2(-a)LAB
整理并代入相关数据得: ![]()
在BC段,考虑到mgsin53o>μmgcos53o,小环一定向下做匀加速直线运动.故要使小环能够运动到C点,只要小环能够运动到B点即可.
设小环到B点时速度为零,根据运动学公式有: ![]()
解得:a’=-12.5m/s2
根据牛顿定律有:mgsin370+μmgcos370=ma′
将a’=12.5m/s2代入上式,解得,μ=0.8125
要使小环能够到达C点,小环和杆之间的动摩擦因数应小于0.8125.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目