Question

如图7-4-9所示，一辆汽车从A点开始爬坡，在牵引力不变的条件下行驶45 m的坡路达到B点时，司机立即关掉油门，以后汽车又向前滑行15 m停在C点，汽车的质量为5×10³ kg，行驶中受到的摩擦力是车重的0.25倍，取g=10 m/s²，求汽车的牵引力做的功和它经过B点时的速率.

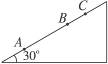
图7-4-9

Answer 1

2.25×10⁴ J  15 m/s

解析:

汽车从A到C的过程中，汽车的发动机牵引力做正功，重力做负功，摩擦力做负功，动能的变化量为零，由动能定理可得：W_F-W_G-f=0

    由于G、F_f已知，汽车的位移也知道，所以有：

    W_F=W_G+=mgh+0.25mgs=2.25×10⁴ J

    汽车由B到C的过程中，克服重力做功，克服摩擦力做功，汽车的动能由mv_b²/2减小到零，列动能定理方程可得：

    -W_G′-=0-mv_B²/2

    即：mv_B²/2=0.25mgs₁+mgs₁ ·sin30°，代入数据可得：v_B=15 m/s.