题目内容
13.宇航员站在某质量分布均匀的星球表面上,从h高度处水平抛出一物体,经时间t落到星球表面上,已知该星球的半径为R,引力常量为G,不计该星球的自转,求:(1)该星球表面的重力加速度g
(2)该星球的质量M
(3)该星球的第一宇宙速度υ1.
分析 (1)小球竖直方向做自由落体,由匀变速运动的速度公式可以求出重力加速度;
(2)根据万有引力等于重力可以求出星球的质量.
(3)该星球的近地卫星的向心力由万有引力提供,该星球表面物体所受重力等于万有引力,联立方程即可求出该星球的第一宇宙速度υ1;
解答 解:(1)小球球竖直方向做自由落体,运动时间:h=$\frac{1}{2}g{t}^{2}$,
解得,星球表面的重力加速度:g=$\frac{2h}{{t}^{2}}$
(2)星球表面的物体受到的重力等于万有引力,即:G$\frac{Mm}{{R}^{2}}$=mg,
解得星球质量:M=$\frac{2h{R}^{2}}{G{t}^{2}}$
(3)卫星绕星球做圆周运动,重力(万有引力)提供向心力,由牛顿第二定律得:
mg=m$\frac{{v}^{2}}{R}$,
解得第一宇宙速度为:v=$\frac{1}{t}\sqrt{2hR}$;
答:(1)该星球表面的重力加速度为$\frac{2h}{{t}^{2}}$;
(2)该星球得质量为$\frac{2h{R}^{2}}{G{t}^{2}}$;
(3)该星球的第一宇宙速度为$\frac{1}{t}\sqrt{2hR}$.
点评 重力加速度g是天体运动研究和天体表面宏观物体运动研究联系的物理量.本题要求学生掌握两种等式:一是物体所受重力等于其吸引力;二是物体做匀速圆周运动其向心力由引力提供.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
3. 某点电荷和金属圆环间的电场线分布如图所示,下列说法正确的是( )
某点电荷和金属圆环间的电场线分布如图所示,下列说法正确的是( )
 某点电荷和金属圆环间的电场线分布如图所示,下列说法正确的是( )
某点电荷和金属圆环间的电场线分布如图所示,下列说法正确的是( )| A. | a点的电势高于b点的电势 | |
| B. | c点的电场强度大于d点的电场强度 | |
| C. | 若将一带正电的试探电荷由a点移到b点,电场力做负功 | |
| D. | 若将一带正电的试探电荷从d点由静止释放,电荷将沿着电场线由d运动到c |
1.蹦极(Bungee Junping)是一项非常刺激的户外休闲活动.设某次跳跃者在蹦极运动场地把长为15m橡皮条一端固定,另一端绑在踝关节处,然后从离地40m高处跳下,跳跃者在空中能够享受到几秒钟的“自由落体”.当人体落到离地面高度为6m时,跳跃者在橡皮绳弹力的作用下开始往上升,假如跳跃者第一次被拉起能达到的最高点在起跳点下方10m处.若跳跃者可视为质点,则从跳跃者起跳到第一次到达最高点的过程中,跳跃者通过的路程和位移大小分别是( )
| A. | 70m、15m | B. | 58m、10m | C. | 43m、10m | D. | 58m、24m |
8. 三颗人造卫星A、B、C绕地球做匀速圆周运动.如图所示,已知mA=mB<mC,则对于三颗卫星,正确的是( )
三颗人造卫星A、B、C绕地球做匀速圆周运动.如图所示,已知mA=mB<mC,则对于三颗卫星,正确的是( )
 三颗人造卫星A、B、C绕地球做匀速圆周运动.如图所示,已知mA=mB<mC,则对于三颗卫星,正确的是( )
三颗人造卫星A、B、C绕地球做匀速圆周运动.如图所示,已知mA=mB<mC,则对于三颗卫星,正确的是( )| A. | 运行线速度关系为vA<vB=vC | |
| B. | 运行周期关系为 TA=TB<TC | |
| C. | 向心力大小关系为 FA=FB>FC | |
| D. | 运行半径与周期关系为$\frac{{{R}_{A}}^{3}}{{{T}_{A}}^{2}}$=$\frac{{{R}_{B}}^{3}}{{{T}_{B}}^{2}}$=$\frac{{{R}_{C}}^{3}}{{{T}_{C}}^{2}}$ |
5.物理学中有多种研究方法,有关研究方法的叙述错误的是( )
| A. | 在伽利略之前的学者们总是通过思辩性的论战决定谁是谁非,是他首先采用了以实验检验猜想和假设的科学方法 | |
| B. | 探究加速度与力、质量之间的定量关系,可以在质量一定的情况下,探究物体的加速度与力的关系;再在物体受力一定的情况下,探究物体的加速度与质量的关系,最后归纳出加速度与力、质量之间的关系.这是物理学中常用的控制变量的研究方法 | |
| C. | 探究作用力与反作用力关系时可以用传感器连在计算机上直接显示力的大小随时间的变化情况,用图象的方法来研究 | |
| D. | 如果电场线与等势面不垂直,那么电场强度就有一个沿着等势面的分量,在等势面上移动电荷时静电力就要做功,这里用的逻辑方法是归纳法 |
 两个相同的白炽灯L1和L2接到如图所示的电路中,灯L1与电容器串联,灯L2与电感线圈串联,当a、b间接交变电压,电路稳定后,保持电压不变只增加交变电压的频率,则L1亮度变亮,L2亮度变暗(填“变亮”或“变亮”“不变”)
两个相同的白炽灯L1和L2接到如图所示的电路中,灯L1与电容器串联,灯L2与电感线圈串联,当a、b间接交变电压,电路稳定后,保持电压不变只增加交变电压的频率,则L1亮度变亮,L2亮度变暗(填“变亮”或“变亮”“不变”) 如图所示,把质量为3g的带电小球B用绝缘细绳悬起,若将带电量为Q=-4.0×10-6C的带电球A靠近B,当两个带电小球在同一高度相距20厘米时,绳与竖直方向成α=30°角,A、B球均静止.试求:B球的带电量及电性.
如图所示,把质量为3g的带电小球B用绝缘细绳悬起,若将带电量为Q=-4.0×10-6C的带电球A靠近B,当两个带电小球在同一高度相距20厘米时,绳与竖直方向成α=30°角,A、B球均静止.试求:B球的带电量及电性.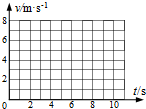 小球从静止开始作匀加速直线运动,第4s末速度达到6m/s,接着匀速运动了7s.在如图所示的坐标平面中作出小球在0-11s内的速度-时间(v-t)图象.
小球从静止开始作匀加速直线运动,第4s末速度达到6m/s,接着匀速运动了7s.在如图所示的坐标平面中作出小球在0-11s内的速度-时间(v-t)图象.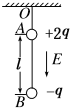 在场强大小为E,方向竖直向下的匀强电场中,有两个质量均为m的带电小球A和B,电荷量分别为+2q和-q,两小球间用长为l的绝缘细线连接,并用绝缘细线悬挂在O点,如图所示.问平衡时,
在场强大小为E,方向竖直向下的匀强电场中,有两个质量均为m的带电小球A和B,电荷量分别为+2q和-q,两小球间用长为l的绝缘细线连接,并用绝缘细线悬挂在O点,如图所示.问平衡时,