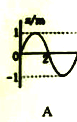��Ŀ����
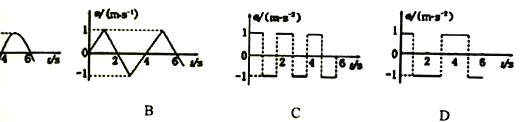
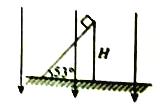
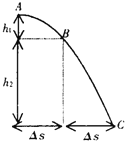
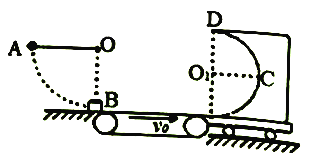
����Ŀ����ͼ��ʾ��С��Aϵ��ϸ�ߵ�һ�ˣ��ߵ���һ�˹̶���O�㣬O���⻬ˮƽ��ľ���Ϊh=0.8m����֪A������Ϊm�����B��������С��A��3�������B����ˮƽ���ʹ���˵�ˮƽ������λ��O�����·������ʹ��Ҷ���һ����Բ�⻬�����С����С����������С��A��5����ˮƽ�桢���ʹ���С�����ϱ���ƽ�����ӣ����B�봫�ʹ���Ķ�Ħ������Ϊ��=0.5������Ħ�����ƣ����ʹ���L=1.5m���Ժ㶨����v=4m/s˳ʱ����ת��������С��Aʹ��ˮƽ��ֱ���ɾ�ֹ�ͷţ�С���˶�����͵�ʱ�����B����������������С�����̶������B�պ��ܻ�����Բ��O1�ȸߵ�C�㣬�������ٶ�gȡ10m/s2��С������������Ϊ�ʵ㡣��
(1)С��A�����B���������B���ٶ�v��С��
(2)�����B������ΪmB=1kg�������B�봫�ʹ�֮����Ħ��������������Q��
(3)С���ϵİ�Բ����뾶R��С��
���𰸡���1��2m/s��2��2J ��3��0.5m
�����������������(1) С��A�°ڽλ�е���غ㣬�ɻ�е���غ㶨�ɽ������͵���ٶȣ�A��B��ײ���ݶ����غ����������ٶȣ�
��2��A�ڴ��ʹ����ȼ��ٺ����������ȱ���ֱ���˶��Ĺ���������λ�Ƹ���Q=fs���Ħ��������������
��3���ɶ����غ��������غ����ľ���Ҷ���B�ľ��롣
�⣺��1��С��A�°ڽλ�е���غ㣬�ɻ�е���غ㶨�ɵã�
![]()
A��B��ײ����ϵͳ�������������غ㣬��A�ij��ٶȷ���Ϊ�����ã�
![]()
![]()
�������ݽ�ã�vB=2m/s��
��2������ʱ��t��B�봫�ʹ��ٶ���ȣ����ȱ���ֱ���˶��ٶȹ�ʽ�ã�
v0=vB+��gt
�������ݽ�ã�t=0.4s
��黬�еľ���Ϊ��![]()
��ã�s��=1.2m
���ʹ���λ��Ϊ��s��=v0t=4��0.4m=1.6m
����S��=S����S��=1.6m��1.2m=0.4m
Q=fS��=��mgS����0.5��1��10��0.4 J =2J ��
(3)����ڴ��ʹ���һֱ���ٵ����Ҷ�ʱǡ���봫�ʹ��ٶ���ȣ�ϵͳˮƽ�������غ㣬������Ϊ�������ɶ����غ㶨�ɵã�
3mv0=��3m+5m��v
�ɻ�е���غ㶨�ɵã�
![]()
�������ݽ�ã�R=0.5m��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�