题目内容
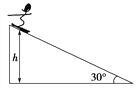
【题目】如图所示,物体从长为16m,倾角为37°的斜面顶端C由静止开始滑下,在斜面底端D用一段光滑的小圆弧滑上输送带AB上的A时速度的大小不变,物体与斜面、物体与输送带间的动摩擦因数均为0.5,输送带以2m/s的速度沿逆时针方向做匀速运动,输送带与水平方向的夹角也为37°,输送带足够长,( sin37°=0.6,cos37°=0.8)g取10m/s2.求

(1)物体在输送带上运动到离A点的最远距离;
(2)物体第一次在输送带上运动的时间;
(3)物体第一次回到斜面上上升的最大高度.
【答案】(1)3.2m(2)2s(3)0.48m
【解析】(1)根据牛顿第二定律得,物体下滑的加速度为:
a1=![]() =gsin37°-μgcos37°=10×0.6﹣0.5×10×0.8m/s2=2m/s2.
=gsin37°-μgcos37°=10×0.6﹣0.5×10×0.8m/s2=2m/s2.
则物体滑到底端的速度为:![]() .
.
物体滑上传送带向上滑动时的加速度为:
a2=![]() =gsin37°+μgcos37°=10×0.6+0.5×10×0.8m/s2=10m/s2,
=gsin37°+μgcos37°=10×0.6+0.5×10×0.8m/s2=10m/s2,
则物体在传送带上运动的最远距离为:![]() .
.
(2)物体向上滑动的时间为:![]() ,
,
物体返回做匀加速运动的加速度为:a3=a2=10m/s2,
速度达到传送带速度的时间为:![]() ,
,
匀加速直线运动的位移为:![]()
速度相等后继续做匀加速运动的加速度为:
a4=![]() =gsin37°﹣μgcos37°=10×0.6﹣0.5×10×0.8m/s2=2m/s2.
=gsin37°﹣μgcos37°=10×0.6﹣0.5×10×0.8m/s2=2m/s2.
继续做匀加速运动的位移为:![]()
代入数据解得:t3=1s,
则t=t1+t2+t3=0.8+0.2+1s=2s
则物体到达底端的速度为:v3=v2+a4t3=2+2×1m/s=4m/s.
(3)物体返回斜面的加速度为:
a5=![]() =gsin37°+μgcos37°=10×0.6+0.5×10×0.8m/s2=10m/s2,
=gsin37°+μgcos37°=10×0.6+0.5×10×0.8m/s2=10m/s2,
则物体回到斜面上上升的位移为:![]() ,
,
则上升的最大高度为:h=x3sin37°=0.8×0.6m=0.48m.