题目内容
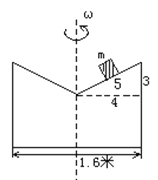
【题目】在直径1.6m的圆柱体一端截出一圆锥,如下图所示,在看到剖面上,三角形的三边之比为3:4:5, 圆柱体可绕其中心对称轴匀速旋转。将一小木块放置在斜面的中点,它与斜面间动摩擦力因素为0.25,若小木块保持在此位置不动,则圆柱体旋转的角速度应为多大.(结果用根式表示;g取10m/s2)
【答案】![]() ≤ω≤
≤ω≤![]()
【解析】当圆柱体旋转角速度最小为![]() 时,木块有沿斜面向下滑动趋势,木块受最大静摩擦力
时,木块有沿斜面向下滑动趋势,木块受最大静摩擦力![]() 的方向沿斜面向上。木块受重力
的方向沿斜面向上。木块受重力![]() 、斜面支持力N和静摩擦
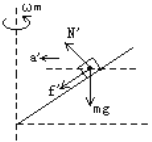
、斜面支持力N和静摩擦![]() ,如图所示:
,如图所示:

木块在水平面内作匀速圆周运动,向心加速度![]() ,
, ![]() 。
。
根据牛顿第二定律得:
水平方向: ![]() ①
①
竖直方向:![]() ② 又
② 又![]() ③
③
联立①、②、③解得![]()
![]() 当圆柱体旋转角速度最大为
当圆柱体旋转角速度最大为![]() 时,木块有沿斜面向上滑动趋势,木块受最大静摩擦力
时,木块有沿斜面向上滑动趋势,木块受最大静摩擦力![]() 的方向沿斜面向下。木块还受重力
的方向沿斜面向下。木块还受重力![]() 和斜面支持力
和斜面支持力![]() 作用,如图所示。木块加速度
作用,如图所示。木块加速度![]() 。
。
由牛顿第二定律得
水平方向: ![]() ④
④
竖直方向:![]() ⑤
⑤
又![]() ⑥
⑥
联立④、⑤、⑥解得
![]() ,
, ![]()
圆柱体旋转的角速度![]() 应为
应为![]() ≤ω≤
≤ω≤![]()

练习册系列答案
相关题目