题目内容
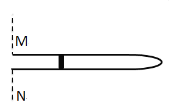
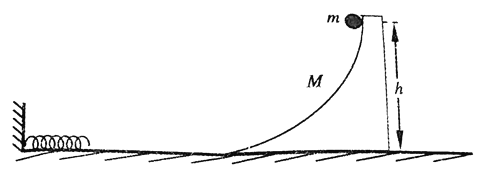
【题目】如图，足够大的光滑水平面上放着质量为M的滑块，质量为m的光滑小球从高h处由静止开始沿滑块的曲面滑下，到达水平面后碰到一端固定在竖直挡板上的轻弹簧后，等速方向弹回。曲面末端切线水平，重力加速度大小为g。求：
（1）弹簧第一次被压缩时的最大弹性势能；
（2）若M=2m，小球再次滑上滑块所能达到的最大高度。
【答案】（1）
（2）
【解析】
（1）根据动量守恒定律和能量守恒关系可求解滑块底端与滑块分离时滑块和小球的速度大小；弹簧被压缩到最短时，小球的动能全部转化为弹簧的弹性势能；（2）小球被弹簧弹回后，沿滑块滑上到达最高点时速度相等，根据动量守恒定律和机械能守恒可得小球再次滑上滑块所能达到的最大高度。
（1）设小球滑到滑块底端与滑块分离时滑块和小球的速度大小分别为V1和v1，取向右为正方向，根据动量守恒定律和能量守恒关系可得：
MV1-mv1=0
弹簧被压缩到最短时，小球的动能全部转化为弹簧的弹性势能：
Epm=
mv12
解得
（2）若M=2m则由（1）中两式可得：
；
小球被弹簧弹回后，沿滑块滑上到达最高点时速度相等，设速度为v，最大高度为H；取向右为正方向，根据动量守恒定律和机械能守恒可得：
MV1+mv1=(M+m)v
解得H=h/9
练习册系列答案
相关题目
