Question

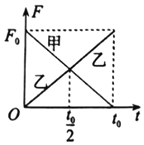
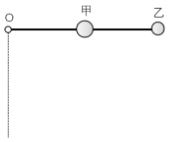
【题目】如图所示，质量不计的细直硬棒长为2L，其一端O点用铰链与固定转轴连接，在细棒的中点固定质量为2m的小球甲，在细棒的另一端固定质量为m小球乙。将棒置于水平位置由静止开始释放，棒与球组成的系统将在竖直平面内做无阻力的转动。则该系统在由水平位置转到竖直位置的过程中（　　）

A.系统的机械能不守恒

B.系统中细棒对乙球做正功

C.甲、乙两球所受的向心力不相等

D.乙球转到竖直位置时的速度比甲球小

Answer 1

【答案】B

【解析】

A．以系统为研究对象，由于只有重力做功，只发生重力势能和动能相互转化，故系统的机械能守恒，A错误；

B．在转动过程中，甲、乙两球的角速度相同，设转到竖直位置时，甲球的速度为v1，乙球的速度为v2，由

同轴转动ω相等，可得

由系统的机械能守恒知系统减少的重力势能等于增加的动能，可得

解得

，

设细棒对乙球做的功为W，根据动能定理得

解得

可见，系统中细棒对乙球做正功，B正确；

C．甲、乙两球所受的向心力分别为

F2＝m＝m＝2m

则

C错误；

D．由上分析知，乙球转到竖直位置时的速度比甲球大，D错误。

故选B。