题目内容
【题目】如图甲所示,水平地面上放置一倾角为θ=37°的足够长的斜面,质量为m的物块置于斜面的底端.某时刻起物块在沿斜面向上的力F作用下由静止开始运动,力F随位移变化的规律如图乙所示.已知整个过程斜面体始终保持静止状态,物块开始运动t=0.5s内位移x1=1m,0.5s后物块再运动x2=2m时速度减为0.取g=10m/s2 , sin37°=0.6,cos37°=0.8.求:
(1)由静止开始,0.5s末物块运动的速度大小v.
(2)物块沿斜面向上运动过程,受到的摩擦力做的功Wf .
(3)物块在沿斜面向下运动过程中,斜面体受到地面的摩擦力.
【答案】
(1)解:)由题意,0.5s内物块做匀加速直线运动,则
![]() a1t2=x1
a1t2=x1
v=a1t
解得:a1=8m/s2,v=4m/s
答:由静止开始,0.5s末物块运动的速度大小v是4m/s.
(2)解:加速和减速过程沿斜面向上的力分别为F1=18N、F2=6N,设物块的质量m和物块与斜面间的动摩擦因数,由动能定理有
加速过程 (F1﹣mgsinθ﹣μmgcosθ)x1= ![]() mv2
mv2
减速过程﹣(mgsinθ+μmgcosθ﹣F2)x2=0﹣ ![]() mv2
mv2
Wf=﹣μmgcosθ(x1+x2)
联立解得:m=1kg,=0.5
Wf=﹣12J
答:物块沿斜面向上运动过程,受到的摩擦力做的功Wf是﹣12J.
(3)解:斜面体受力如图
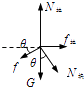
受到物块的压力N块=mgcosθ
受到物块的摩擦力f=μmgcosθ
设斜面体受到沿地面向右的摩擦力为f地,由平衡条件有
f地+N块sinθ﹣fcosθ=0
解得:f地=﹣1.6N,负号表示方向水平向左.
答:物块在沿斜面向下运动过程中,斜面体受到地面的摩擦力大小为1.6N,方向水平向左.
【解析】(1)先分析物体的运动情况:0.5s内物块做匀加速直线运动,0.5s后物块做匀减速直线运动.研究0.5s内物体的运动过程:已知时间、初速度和位移,根据位移时间公式可求得加速度,由速度时间公式可求得0.5s末物块运动的速度大小v.(2)对于加速和减速过程分别运用动能定理,列方程,即可求得摩擦力做的功Wf.(3)物块在沿斜面向下运动过程中,斜面体静止不动,合力为零,分析其受力情况,运用平衡条件求解即可.
【考点精析】认真审题,首先需要了解动能定理的综合应用(应用动能定理只考虑初、末状态,没有守恒条件的限制,也不受力的性质和物理过程的变化的影响.所以,凡涉及力和位移,而不涉及力的作用时间的动力学问题,都可以用动能定理分析和解答,而且一般都比用牛顿运动定律和机械能守恒定律简捷).






