题目内容
如图所示，在水平向右的匀强电场中，用长为L的绝缘细绳将一个质量为m的带电小球悬挂于O点，平衡时，小球位于B点，此时绳与竖直方向的夹角为θ（θ＜45°）．已知重力加速度为g．求：（1）小球静止在B点时受到绳的拉力大小．
（2）若将小球拉到O点等高的A点（此时绳拉直），然后释放小球，当小球运动到最低点C时受到绳的拉力大小．
分析：（1）根据受力分析，并由力的平行四边形定则，结合三角函数，即可求解；
（2）根据动能定理，结合牛顿第二定律，即可求解．
（2）根据动能定理，结合牛顿第二定律，即可求解．
解答：解：（1）在B点，T1cosθ=mg
∴T1=
T1 sinθ=qE
∴qE=mgtanθ
（2）从A到C，根据动能定理，
则有 mgL-qEL=
mv2
又T2-mg=m
由以上解得 T2=mg （3-2tanθ）
答：（1）小球静止在B点时受到绳的拉力大小
．
（2）若将小球拉到O点等高的A点（此时绳拉直），然后释放小球，当小球运动到最低点C时受到绳的拉力大小mg （3-2tanθ）．
∴T1=
| mg |
| cosθ |
T1 sinθ=qE
∴qE=mgtanθ
（2）从A到C，根据动能定理，
则有 mgL-qEL=
| 1 |
| 2 |
又T2-mg=m
| v2 |
| L |
由以上解得 T2=mg （3-2tanθ）
答：（1）小球静止在B点时受到绳的拉力大小
| mg |
| cosθ |
（2）若将小球拉到O点等高的A点（此时绳拉直），然后释放小球，当小球运动到最低点C时受到绳的拉力大小mg （3-2tanθ）．
点评：考查如何受力分析，掌握力的平行四边形定则、动能定理及牛顿第二定律的应用，注意做功的正负．
练习册系列答案
相关题目
如图所示，在水平向右的拉力F作用下，木块在长木板上向右做匀减速直线运动，加速度大小为a．长木板处于静止状态．已知，木块质量为m，长木板质量为M，长木板与水平地面间的动摩擦因数为μ1，木块与长木板间的动摩擦因数为μ2．地面对长木板的摩擦力大小为（ ）
如图所示，在水平向右的匀强电场中，用长为L的绝缘细绳将一个质量为m的带电小球悬挂于O点，平衡时，小球位于B点，此时绳与竖直方向的夹角为θ（θ＜45°）．已知重力加速度为g．求：小球静止在B点时受到绳的拉力大小．
如图所示，在水平向右场强为E的匀强电场中，有一质量为m、电荷量为+q的点电荷从A点由静止释放，在电场力的作用下经时间t运动到B点．求：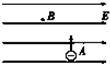
如图所示，在水平向右的匀强电场中的A点，有一个质量为m、带电荷量为-q的油滴以速度v竖直向上运动．已知当油滴经过最高点B时，速度大小也为v．求：