题目内容
对于两物体碰撞前后速度在同一直线上,且无机械能损失的碰撞过程,可以简化为如下模型:A、B两物体位于光滑水平面上,仅限于沿同一直线运动.当它们之间的距离大于等于某一定值d时,相互作用力为零;当它们之间的距离小于d时,存在大小恒为F的斥力.设A物体质量m=1.0 kg,开始时静止在直线上某点;B物体质量m2=3.0 kg,以速度v0从远处沿该直线向A运动,如图所示.若d=0.10 m,F=0.60 N,v0=0.20 m/s,求: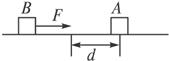
(1)相互作用过程中A、B加速度的大小;
(2)从开始相互作用到A、B间的距离最小时,系统(物体组)动能的减少量;
(3)A、B间的最小距离.
(1)a1=0.6 m/s2 a2=0.20 m/s2(2)0.15 J (3)0.075 m
解析:(1)a1=![]() =0.6 m/s2,a2=
=0.6 m/s2,a2=![]() =0.20 m/s2.
=0.20 m/s2.
(2)两者速度相同的距离最近,设此时的速度为v,由动量守恒m2v0=(m1+m2)v
可得:v=![]() =0.15 m/s
=0.15 m/s
所以ΔEk=![]() m2v02-
m2v02-![]() (m1+m2)v2=0.015 J.
(m1+m2)v2=0.015 J.
(3)设从开始相互作用到A、B距离最近物体B通过的距离为sB,物体A通过的距离为sA,A、B距离最近为dmin,则有:dmin=d-(sB-sA) ①
利用动能定理分别对A、B列方程有:
FsB=![]() m2v02-
m2v02-![]() m2v2 ②
m2v2 ②
FsA=![]() m1v2 ③
m1v2 ③
由以上①②③式,可得:dmin=0.075 m.

练习册系列答案
相关题目
 对于两物体碰撞前后速度在同一直线上,且无机械能损失的碰撞过程,可以简化为如下模型:A、B两物体位于光华水平面上,仅限于沿同一条直线云动.当他们之间的距离大于等于某一定值d时,互相作用力为零;当他们之间的距离小于d时,存在大小恒为F的斥力.设A物体质量m1=1.0kg,开始时净止在直线上某点;B物体质量m2=3.0kg以速度v0从远处沿直线向A运动,如图所示.若d=0.10m,F=0.60N.v0=0.20/s,求:
对于两物体碰撞前后速度在同一直线上,且无机械能损失的碰撞过程,可以简化为如下模型:A、B两物体位于光华水平面上,仅限于沿同一条直线云动.当他们之间的距离大于等于某一定值d时,互相作用力为零;当他们之间的距离小于d时,存在大小恒为F的斥力.设A物体质量m1=1.0kg,开始时净止在直线上某点;B物体质量m2=3.0kg以速度v0从远处沿直线向A运动,如图所示.若d=0.10m,F=0.60N.v0=0.20/s,求: (2008?东莞模拟)对于两物体碰撞前后速度在同一直线上,且无机械能损失的碰撞过程,可以简化为如下模型:A、B两物体位于光滑水平面上,仅限于沿同一直线运动,当它们之间的距离大于等于某一定值d时,相互作用力为零;当它们之间的距离小于d时,存在大小恒为F的斥力,设A物体质量m1=1.0kg,开始时静止在直线上某点;B物体质量m2=3.0kg,以速度v0从远处沿该直线向A 运动,如图所示,若F=0.60N,v0=0.20m/s,求:
(2008?东莞模拟)对于两物体碰撞前后速度在同一直线上,且无机械能损失的碰撞过程,可以简化为如下模型:A、B两物体位于光滑水平面上,仅限于沿同一直线运动,当它们之间的距离大于等于某一定值d时,相互作用力为零;当它们之间的距离小于d时,存在大小恒为F的斥力,设A物体质量m1=1.0kg,开始时静止在直线上某点;B物体质量m2=3.0kg,以速度v0从远处沿该直线向A 运动,如图所示,若F=0.60N,v0=0.20m/s,求: A、B间的最小距离
A、B间的最小距离 =1.0kg,开始时静止在直线上某点;B物体质量
=1.0kg,开始时静止在直线上某点;B物体质量 =3.0kg,以速度
=3.0kg,以速度 从远处沿该直线向A运动,如图所示。若d=0.10m,F=0.60N,
从远处沿该直线向A运动,如图所示。若d=0.10m,F=0.60N,