题目内容
5．
如图所示，光滑水平面OB与足够长粗糙斜面BC交于B点，水平面和斜面平滑相连，一轻弹簧左端固定于竖直墙面．现将滑块1压缩弹簧至D点，然后由静止释放，滑块脱离弹簧后经B点滑上斜面，上升到最大高度，并静止在斜面上；换用相同材料的滑块2，压缩弹簧到相同位置，然后由静止释放，上升到最大高度．下列说法正确的是（ ）| A． | 质量大的滑块上升到最高点克服重力做的功多 | |
| B． | 两滑块上升到最高点克服重力做的功相同，与它们的质量大小无关 | |
| C． | 质量小的滑块上升到最高点损失的机械能少 | |
| D． | 两滑块上升到最高点损失的机械能相同，与它们的质量大小无关 |
分析 释放弹簧后，先是弹性势能转化为动能，滑块冲上斜面运动过程机械能损失变为摩擦生热，由能量守恒定律可得，动能的减少等于重力势能的增加量与摩擦产生的热量之和．根据能量转化和守恒定律分析．
解答 解：AB、设滑块上升的最大高度为h，由能量守恒定律得：EP=mgh+μmgcosθ×$\frac{h}{sinθ}$，所以，mgh=$\frac{{E}_{p}}{1+μcotθ}$，由于开始的弹性势能相同，可知克服重力做的功相同，与它们的质量大小无关，故A错误，B正确．
C、由于开始的弹性势能相同，最终滑块的重力势能相同，所以每个滑块机械能损失相同，与滑动的质量无关．故C错误，D正确．
故选：BD．
点评 解决本题的关键是会应用能量守恒定律解决问题，同时要推理能力．对于A项不能简单地认为质量越大，物体克服重力做的功多，应列式半定量分析．
练习册系列答案
相关题目
15．
如图，为由两个振动情况完全相同的振源发出的两列波在空间相遇而叠加所产生的图样，每列波振幅均为A，其中实线表示波峰，虚线表示波谷，则关于介质中的a、b、c、d四点，（b、c为相邻波峰和波谷的中点）下列说法正确的是（ ）
如图，为由两个振动情况完全相同的振源发出的两列波在空间相遇而叠加所产生的图样，每列波振幅均为A，其中实线表示波峰，虚线表示波谷，则关于介质中的a、b、c、d四点，（b、c为相邻波峰和波谷的中点）下列说法正确的是（ ）| A． | a、c振幅为2A，b、d始终不动 | |
| B． | 图示时刻d点位移大小为2A，b、c、d三点位移为零 | |
| C． | a点位移大小始终为2A，d点位移始终为零 | |
| D． | 这四个点全部是振动减弱点 |
16．关于力对物体做功，下列说法中正确的是（ ）
| A． | 合外力对物体不做功，物体一定做匀速直线运动 | |
| B． | 滑动摩擦力和静摩擦力都可以对物体做正功或负功 | |
| C． | 不论怎样的力对物体做功，都可以用W=Fscos α来计算 | |
| D． | 一对作用力和反作用力在相同时间内做的功一定大小相等、正负相反 |
20．
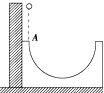如图所示，将一个内外侧均光滑的半圆形槽置于光滑的水平面上，槽的左侧有一竖直墙壁．现让一小球自左端槽口A点的正上方由静止开始下落，从A点与半圆形槽相切进入槽内，不计空气阻力，下列说法正确的是（ ）
如图所示，将一个内外侧均光滑的半圆形槽置于光滑的水平面上，槽的左侧有一竖直墙壁．现让一小球自左端槽口A点的正上方由静止开始下落，从A点与半圆形槽相切进入槽内，不计空气阻力，下列说法正确的是（ ）| A． | 小球从开始下落至运动到半圆形槽最低点的过程中，重力的功率越来越大 | |
| B． | 小球从开始下落到从右侧离开槽的过程中，小球的机械能守恒 | |
| C． | 小球从右侧离开半圆形槽后，能上升到与开始下落位置高度相同的地方 | |
| D． | 小球从刚进入半圆形槽到从右侧离开槽的过程中，小球与槽组成的系统机械能守恒 |
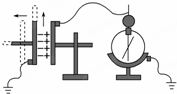用如图所示装置可以研究影响平等板电容器电容的因素，设两极板正对面积为S，两极板间的距离为d，板间电介质的介电常数为?，静电计指针偏角为θ，实验中，极板所带电荷量不变，