题目内容
2. 如图所示,在0≤x≤3a、0≤y≤a范围内有垂直于xy平面向外的匀强磁场,磁感应强度大小为B坐标,原点O处有一个粒子源,朝第一象限各个方向发射大量各种速度的某种带正电粒子,已知粒子质量为m,电荷量为q,不计粒子重力.
如图所示,在0≤x≤3a、0≤y≤a范围内有垂直于xy平面向外的匀强磁场,磁感应强度大小为B坐标,原点O处有一个粒子源,朝第一象限各个方向发射大量各种速度的某种带正电粒子,已知粒子质量为m,电荷量为q,不计粒子重力.(1)若所有粒子都无法从CD边射出,求粒子速度的最大值:
(2)对于能从C点射出磁场的粒子,求在磁场中运动的最长时间(.可用反三角函数丧示)
分析 (1)临界情况是轨迹圆与AC边相切且粒子从D点射出,画出轨迹,结合几何关系得到轨道半径,根据牛顿第二定律列式求解出最大速度;
(2)能够从C点射出的粒子,如果速度最大,则轨道半径最小,对应的圆心角最大,临界情况是轨迹与AC相切且经过C点,画出轨迹,结合几何关系得到轨道半径,根据t=$\frac{θ}{2π}T$求解时间.
解答 解:(1)画出临界轨迹,如图所示: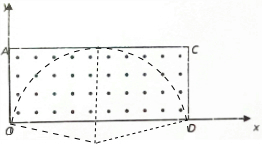
结合几何关系,有:
R2=(1.5a)2+(R-a)2
解得:
R=1.625a
根据牛顿第二定律,有:
qvB=m$\frac{{v}^{2}}{R}$
联立解得:
$v=\frac{13qBa}{8m}$
(2)当轨迹与AC相切且经过C点时,在磁场中运动的时间最长,轨迹如图: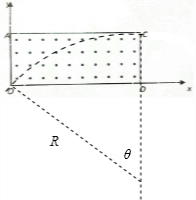
结合几何关系,有:
R2=(3a)2+(R-a)2
解得:
R=5a
根据牛顿第二定律,有:
qvB=m$\frac{{v}^{2}}{R}$
联立解得:
$v=\frac{5qBa}{m}$
sinθ=$\frac{3a}{R}=0.6$
故θ=37°=$\frac{37°}{360°}×2π$≈0.65rad
故运动时间为:
t=$\frac{θR}{v}$=$\frac{0.65×5a}{\frac{5qBa}{m}}$=$\frac{0.65m}{qB}$
答:(1)若所有粒子都无法从CD边射出,粒子速度的最大值为$\frac{13qBa}{8m}$;
(2)对于能从C点射出磁场的粒子,在磁场中运动的最长时间为$\frac{0.65m}{qB}$.
点评 本题关键是明确粒子的运动规律,找出临界轨迹,结合几何关系求解轨道半径,结合牛顿第二定律列式求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.以下叙述正确的是( )
| A. | 库仑提出了分子电流假说 | |
| B. | 首先发现电流周围存在磁场的著名科学家是奥斯特 | |
| C. | 首先提出磁场对运动电荷有力的作用的科学家是安培 | |
| D. | 感应电流遵从楞次定律所描述的方向,这是能量守恒定律的必然结果 |
2.汽车从静止开始作匀变速直线运动,第4秒末关闭发动机,再经6秒停止,汽车一共行驶了40米则( )
| A. | 在运动过程中的最大速度为8m/s | |
| B. | 在运动过程中的最大速度为5m/s | |
| C. | 加速阶段的加速度的大小为2m/s2 | |
| D. | 减速阶段的加速度的大小为1.5m/s2 |
6. 如图所示,将一个表面光滑的铁球放在两块斜面板AB和CD之间,两板与水平面的夹角都是60°.已知重力加速度大小为g,不计空气阻力,则( )
如图所示,将一个表面光滑的铁球放在两块斜面板AB和CD之间,两板与水平面的夹角都是60°.已知重力加速度大小为g,不计空气阻力,则( )
 如图所示,将一个表面光滑的铁球放在两块斜面板AB和CD之间,两板与水平面的夹角都是60°.已知重力加速度大小为g,不计空气阻力,则( )
如图所示,将一个表面光滑的铁球放在两块斜面板AB和CD之间,两板与水平面的夹角都是60°.已知重力加速度大小为g,不计空气阻力,则( )| A. | 如果突然撤去CD板,则撤去后铁球对AB板的压力减小 | |
| B. | 如果突然撤去CD板,则撤去后铁球对AB板的压力增大 | |
| C. | 如果保持AB板不动,使CD板与水平面的夹角缓慢减小,则球对AB板的压力先减小后增大 | |
| D. | 如果保持AB板不动,使CD板与水平面的夹角缓慢减小,则球对CD板的压力先减小后增大 |
11. 如图所示电路中,电源电动势为E,内阻为r,电路中O点接地,当滑动变阻器的滑动片P向右滑动时,M、N两点的电势变化情况是:( )
如图所示电路中,电源电动势为E,内阻为r,电路中O点接地,当滑动变阻器的滑动片P向右滑动时,M、N两点的电势变化情况是:( )
 如图所示电路中,电源电动势为E,内阻为r,电路中O点接地,当滑动变阻器的滑动片P向右滑动时,M、N两点的电势变化情况是:( )
如图所示电路中,电源电动势为E,内阻为r,电路中O点接地,当滑动变阻器的滑动片P向右滑动时,M、N两点的电势变化情况是:( )| A. | 都升高 | |
| B. | 都降低 | |
| C. | M点电势升高,N点电势降低 | |
| D. | M点电势的改变量大于N点电势的改变量 |
12.“神舟七号”载人飞船发射升空后,飞行了2天20小时27分钟,绕地球运行45圈,返回舱顺利返回着陆.这标志着我国航天事业又迈上了一个新台阶,假定正常运行的神舟七号飞船和通信卫星(同步卫星)做的都是匀速圆周运动,下列说法正确的是( )
| A. | 飞船的线速度比通信卫星的线速度小 | |
| B. | 飞船的角速度比通信卫星的角速度小 | |
| C. | 飞船的运行周期比通信卫星的运行周期小 | |
| D. | 飞船的向心加速度比通信卫星的向心加速度小 |

 如图所示,水平放置的平行金属板A和B间的距离为d,极长L=$\sqrt{3}$d,B板的右侧边缘恰好是倾斜挡板NM上的一个小孔K,NM与水平挡板NP成60°角,K与N间的距离$\overline{KN}$=a.现有一质量为m、电荷量为q的带正电的粒子,从AB的中点O以平行于金属板方向OO′的速度v0射入,不计粒子的重力.现在A、B板上加一恒定电压,则该粒子穿过金属板后恰好穿过小孔K:
如图所示,水平放置的平行金属板A和B间的距离为d,极长L=$\sqrt{3}$d,B板的右侧边缘恰好是倾斜挡板NM上的一个小孔K,NM与水平挡板NP成60°角,K与N间的距离$\overline{KN}$=a.现有一质量为m、电荷量为q的带正电的粒子,从AB的中点O以平行于金属板方向OO′的速度v0射入,不计粒子的重力.现在A、B板上加一恒定电压,则该粒子穿过金属板后恰好穿过小孔K: