题目内容
19.正负电子对撞机是使正负电子以相同速率对撞(撞前速度在同一直线上的碰撞)并进行高能物理研究的实验装置(如图甲),该装置一般由高能加速器(同步加速器或直线加速器)、环形储存室(把高能加速器在不同时间加速出来的电子束进行积累的环形真空室)和对撞测量区(对撞时发生的新粒子、新现象进行测量)三个部分组成.为了使正负电子在测量区内不同位置进行对撞,在对撞测量区内设置两个方向相反的匀强磁场区域.对撞区域设计的简化原理如图乙所示:MN和PQ为足够长的竖直边界,水平边界EF将整个区域分成上下两部分,Ⅰ区域的磁场方向垂直纸面向内,Ⅱ区域的磁场方向垂直纸面向外,磁感应强度大小均为B.现有一对正负电子以相同速率分别从注入口C和注入口D同时水平射入,在对撞测量区发生对撞.已知两注入口到EF的距离均为d,边界MN和PQ的间距为L,正电子的质量为m,电量为+e,负电子的质量为m,电量为-e.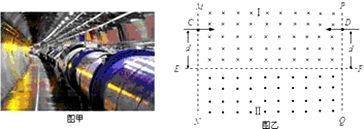
(1)试判断从注入口C入射的是正电子还是负电子;
(2)若L=4$\sqrt{3}$d,要使正负电子经过水平边界EF一次后对撞,求正负电子注入时的初速度大小;
(3)若只从注入口C射入电子,间距L=13(2-$\sqrt{3}$)d,要使电子从PQ边界飞出,求电子射入的最小速率,及以此速度入射到从PQ边界飞出所需的时间.
分析 (1)根据左手定则判断出粒子的电性;
(2)根据几何关系求出半径,根据洛伦兹力提供向心力求出电子注入时的初速度
(3)要使电子从PQ边界飞出,设电子束的最小速率为v,运动的半径为r,画出运动的轨迹,然后结合几何关系与洛伦兹力提供向心力即可求出;
解答  解:(1)负电子(因为电子要向下偏转)
解:(1)负电子(因为电子要向下偏转)
(2)粒子运动轨迹如图所示,根据几何关系有:$(R-d)_{\;}^{2}+(\sqrt{3}d)_{\;}^{2}={R}_{\;}^{2}$
解得:R=2d
根据洛伦兹力提供向心力,有:$qvB=\frac{{m{v^2}}}{R}$
解得:$v=\frac{2eBd}{m}$
(3)要使电子从PQ边界飞出,设电子束的最小速率为v,运动的轨道半径为r,画出运动的轨迹如图所示
由几何关系得: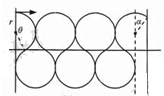 r+rcos30°=d
r+rcos30°=d
即:$r=2(2-\sqrt{3})d$
由圆周运动:$evB=m\frac{{v}_{\;}^{2}}{r}$
代入得:$v=\frac{2(2-\sqrt{3})edB}{m}$
根据题意,设电子在Ⅰ区磁场的区域中运动对应的圆心角为θ,经过3次重复,最后运动的轨迹对应的圆心角为α,设电子在磁场中运动的周期为T,在磁场中运动的时间为t,则:$θ=\frac{5π}{6}$
$α=\frac{π}{6}$
$T=\frac{2πm}{qB}$
得:$t=12×\frac{θ}{2π}T+\frac{α}{2π}T=\frac{61m}{6eB}$
答:(1)试判断从注入口C入射的是负电子;
(2)若L=4$\sqrt{3}$d,要使正负电子经过水平边界EF一次后对撞,正负电子注入时的初速度大小$\frac{2eBd}{m}$;
(3)若只从注入口C射入电子,间距L=13(2-$\sqrt{3}$)d,要使电子从PQ边界飞出,电子射入的最小速率为$\frac{2(2-\sqrt{3})edB}{m}$,及以此速度入射到从PQ边界飞出所需的时间为$\frac{61m}{6eB}$.
点评 主要考查了带电粒子在匀强磁场中运动的问题,要求同学们能正确分析粒子的运动情况,会应用几何知识找到半径,熟练掌握圆周运动基本公式.

| A. | 甲比乙先着地 | B. | 甲比乙的加速度大 | ||
| C. | 甲与乙同时着地 | D. | 甲比乙落地速度大 |
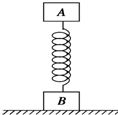 如图所示,质量相等的两木块中间连有一弹簧,今用力F缓慢向上提A,直到B恰好离开地面.开始时物体A静止在弹簧上面.设开始时弹簧的弹性势能为Ep1,B刚要离开地面时,弹簧的弹性势能为Ep2,则关于Ep1、Ep2大小关系及弹性势能变化△Ep说法中正确的是( )
如图所示,质量相等的两木块中间连有一弹簧,今用力F缓慢向上提A,直到B恰好离开地面.开始时物体A静止在弹簧上面.设开始时弹簧的弹性势能为Ep1,B刚要离开地面时,弹簧的弹性势能为Ep2,则关于Ep1、Ep2大小关系及弹性势能变化△Ep说法中正确的是( )| A. | Ep1=Ep2 | B. | Ep1>Ep2 | C. | △Ep>0 | D. | △Ep<0 |
| A. | 物体没做功,则物体就没有能量 | |
| B. | 动摩擦力只能做负功 | |
| C. | 重力对物体做功,物体的重力势能可能增加 | |
| D. | 重力对物体做功,物体的重力势能一定减少 |
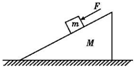 如图所示,一质量为m的物体恰能在质量为M的斜面上匀速下滑,斜面保持静止.现用一沿斜面向下的外力F推此物体,使物体加速下滑;设此过程中斜面受到地面的摩擦力为f,支持力为N,则下列说法正确的是( )
如图所示,一质量为m的物体恰能在质量为M的斜面上匀速下滑,斜面保持静止.现用一沿斜面向下的外力F推此物体,使物体加速下滑;设此过程中斜面受到地面的摩擦力为f,支持力为N,则下列说法正确的是( )| A. | f为零,N=(m+M)g | B. | f不为零,N=(m+M)g | C. | f不为零,N>(m+M)g | D. | f为零,N<(m+M)g |
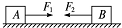 如图所示,在光滑水平面上有两个静止物体A和B,B的质量大于A的质量,现用大小相等、方向相反且在同一直线上的两个力F 1和F 2分别同时作用在这两个物体上,经过相等的时间后撤去两力,又经过一段时间A、B两物体相撞并连为一体,这时A、B将( )
如图所示,在光滑水平面上有两个静止物体A和B,B的质量大于A的质量,现用大小相等、方向相反且在同一直线上的两个力F 1和F 2分别同时作用在这两个物体上,经过相等的时间后撤去两力,又经过一段时间A、B两物体相撞并连为一体,这时A、B将( )| A. | 停止 | B. | 向右运动 | ||
| C. | 向左运动 | D. | 运动方向不能确定 |
 踩板跳水运动员(可看作质点),速度与时间关系图象如图所示,t=0是其向上起跳瞬间,下列说法正确的是( )
踩板跳水运动员(可看作质点),速度与时间关系图象如图所示,t=0是其向上起跳瞬间,下列说法正确的是( )| A. | t1 时刻开始进入水面 | |
| B. | t2 时刻到达最高点 | |
| C. | t3 时刻已浮出水面 | |
| D. | 0~t2 时间内,运动员一直处于失重状态 |
| A. | 重力对小球做的功等于-mgh | B. | 小球落地时的机械能会变大 | ||
| C. | 合外力对小球做的功为4mv2 | D. | 小球克服空气阻力做的功为mv2 |
 某娱乐性比赛项目场地设施如图所示,水平直轨道上安装有可以载人的电动悬挂器,水面上固定一铺有海绵垫的大圆盘,半径R=1m,圆盘的圆心离平台的水平距离为L=8m,圆盘厚度不计,平台距水面高度为H=3.2m,选手在平台上双手抓住悬挂器,在电动机带动下以vo=4m/s匀速运动.在某次体验中,选手在合适的位置松手后恰能落在圆盘的圆心处(选手可看作质点,g=10m/s2).求:
某娱乐性比赛项目场地设施如图所示,水平直轨道上安装有可以载人的电动悬挂器,水面上固定一铺有海绵垫的大圆盘,半径R=1m,圆盘的圆心离平台的水平距离为L=8m,圆盘厚度不计,平台距水面高度为H=3.2m,选手在平台上双手抓住悬挂器,在电动机带动下以vo=4m/s匀速运动.在某次体验中,选手在合适的位置松手后恰能落在圆盘的圆心处(选手可看作质点,g=10m/s2).求: