Question

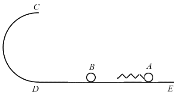
【题目】如图所示，CDE为光滑的轨道，其中ED段是水平的，CD段是竖直平面内的半圆，与ED相切于D点，且半径R=0.5m。质量m=0.2kg的小球B静止在水平轨道上，另一质量M=0.2kg的小球A前端装有一轻质弹簧，以速度v0向左运动并与小球B发生相互作用。小球A、B均可视为质点，若小球B与弹簧分离后滑上半圆轨道，并恰好能过最高点C，弹簧始终在弹性限度内，取重力加速度g=10m/s2，求：

（1）小球B与弹簧分离时的速度vB多大；

（2）小球A的速度v0多大；

（3）弹簧最大的弹性势能EP是多少？

Answer 1

【答案】（1）vB=5m/s；（2）v0=5m/s；（3）EP=1.25J

【解析】

（1）设小球B恰好过C点时速度为vC，则有

①

②

联立①②解得：vB=5m/s

（2）小球B与弹簧分离前后，小球A、B及弹簧系统：由动量守恒定律及能量守恒定律有

③

④

联立③④解得：v0=5m/s

（3）小球A、B及弹簧系统：当A、B两者速度相同时，弹簧有最大弹性势能Ep，设共同速度为v，由动量守恒定律及能量守恒定律有

⑤

⑥

联立⑤⑥解得：EP=1.25J