题目内容
（2011?无锡一模）在直径为d的圆形区域内存在着均匀磁场，磁感应强度为B，磁场方向垂直于纸面向外．一电荷量为q、质量为m的带正电粒子，从磁场区域的一条直径AC上的A点沿纸面射入磁场，其速度方向与AC成α=30°角，如图所示，若此粒子在磁场区域运动过程中速度的方向改变了120°，粒子的重力忽略不计，求：（1）该粒子在磁场区域内运动所用的时间t；
（2）该粒子射入时的速度大小v．
分析：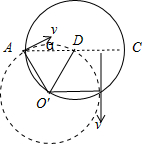
带电粒子在磁场中的运动其速度偏转角等于对应的圆心角，周期T=
，则运动时间t=
T；由题意得结合几何关系，可求圆周运动的半径R与d的关系，由洛伦兹力提供向心力可求v．
带电粒子在磁场中的运动其速度偏转角等于对应的圆心角，周期T=| 2πm |
| qB |
| θ |
| 2π |
解答：解：（1）带电粒子在磁场中的运动周期T=
，运动时间t=
T=
=
（2）由几何关系得：三角形ADO′为等边三角形，R=
根据qvB=m
得：v=
答：（1）该粒子在磁场区域内运动所用的时间为
；
（2）该粒子射入时的速度大小为
．
| 2πm |
| qB |
| θ |
| 2π |
| ||
| 2π |
| 2πm |
| qB |
| 2πm |
| 3qB |
（2）由几何关系得：三角形ADO′为等边三角形，R=
| d |
| 2 |
根据qvB=m
| v2 |
| R |
| qBd |
| 2m |
答：（1）该粒子在磁场区域内运动所用的时间为
| 2πm |
| 3qB |
（2）该粒子射入时的速度大小为
| qBd |
| 2m |
点评：考查了带电离子在磁场中的运动，会定圆心、找半径，结合圆周运动求相关量．
练习册系列答案
相关题目
（2011?无锡一模）质量为0.3kg的物体在水平面上运动，图中的两条直线分别表示物体受水平拉力和不受水平拉力的v-t图象，则下列说法中正确的是（ ）
（2011?无锡一模）小明站在水平地面上，手握不可伸长的轻绳一端，绳的另一端系有质量为m的小球，甩动手腕，使球在竖直平面内做圆周运动．当球某次运动到最低点时，绳突然断掉，球飞行水平距离d后落地．如题图所示．已知握绳的手离地面高度为d，手与球之间的绳长为
（2011?无锡一模）在“用电流表和电压表测定电池的电动势和内电阻”的实验中．
（2011?无锡一模）如图所示是一个玩具陀螺，a、b、c是陀螺表面上的三点．当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时，下列表述正确的是（ ）
（2011?无锡一模）回旋加速器是用来加速带电粒子的装置，如图所示．它的核心部分是两个D形金属盒，两盒相距很近，分别和高频交流电源相连接，两盒间的窄缝中形成匀强电场，使带电粒子每次通过窄缝都得到加速．两盒放在匀强磁场中，磁场方向垂直于盒底面，带电粒子在磁场中做圆周运动，通过两盒间的窄缝时反复被加速，直到达到最大圆周半径时通过特殊装置被引出．如果用同一回旋加速器分别加速氚核（13H）和α粒子（24He）比较它们所加的高频交流电源的周期和获得的最大动能的大小，有（ ）